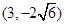题目内容
求满足下列条件的椭圆的标准方程:
(1)经过点(2,-3)且与椭圆9x2+4y2=36有公共焦点;
(2)经过点A(2,
)和点B(
,1).
(1)经过点(2,-3)且与椭圆9x2+4y2=36有公共焦点;
(2)经过点A(2,
| 2 |
| 6 |
分析:(1)由椭圆9x2+4y2=36的焦点为F(0,±
),设所求椭圆的方程为
+
=1,把点(2,-3)代入,得
+
=1,由此能求出椭圆方程.
(2)设所求的椭圆方程为mx2+ny2=1,(m>0,n>0,m≠n),由椭圆经过点A(2,
)和点B(
,1),知
,由此能求出椭圆方程.
| 5 |
| x2 |
| a2-5 |
| y2 |
| a2 |
| 4 |
| a2-5 |
| 9 |
| a2 |
(2)设所求的椭圆方程为mx2+ny2=1,(m>0,n>0,m≠n),由椭圆经过点A(2,
| 2 |
| 6 |
|
解答:解:(1)∵椭圆9x2+4y2=36的焦点为F(0,±
),
∴设所求椭圆的方程为
+
=1,
把点(2,-3)代入,得
+
=1,
整理,得a4-18a2+45=0,
解得a2=15,或a2=3(舍).
∴所求的椭圆方程为
+
=1.
(2)设所求的椭圆方程为mx2+ny2=1,(m>0,n>0,m≠n)
∵椭圆经过点A(2,
)和点B(
,1),
∴
,
解得m=
,n=
,
∴所求的椭圆方程为
+
=1.
| 5 |
∴设所求椭圆的方程为
| x2 |
| a2-5 |
| y2 |
| a2 |
把点(2,-3)代入,得
| 4 |
| a2-5 |
| 9 |
| a2 |
整理,得a4-18a2+45=0,
解得a2=15,或a2=3(舍).
∴所求的椭圆方程为
| x2 |
| 10 |
| y2 |
| 15 |
(2)设所求的椭圆方程为mx2+ny2=1,(m>0,n>0,m≠n)
∵椭圆经过点A(2,
| 2 |
| 6 |
∴
|
解得m=
| 1 |
| 8 |
| 1 |
| 4 |
∴所求的椭圆方程为
| x2 |
| 8 |
| y2 |
| 4 |
点评:本题考查椭圆方程的求法,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
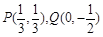 ;
;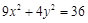 具有共同的焦点.
具有共同的焦点.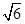 ),Q(
),Q(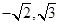 ). (2)焦点在x轴上,焦距为4,并且过点
). (2)焦点在x轴上,焦距为4,并且过点