题目内容
(本小题满分12分) 求满足下列条件的椭圆的标准方程.
(1)焦点在坐标轴上,且经过两点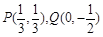 ;
;
(2)经过点(2,-3)且与椭圆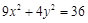 具有共同的焦点.
具有共同的焦点.
【答案】
(1) 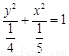 。(2)
。(2)  。
。
【解析】本题主要考查利用椭圆的定义与椭圆的简单性质求椭圆的标准方程,解决此类问题的步骤是:首先确定标准方程的形式(焦点在x轴还是再y轴上),再根据条件求出 a,b,然后写出椭圆的方程,此题属于基础题.
(1)当所求椭圆的焦点在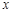 轴上时,设它的标准方程为
轴上时,设它的标准方程为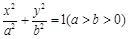 ,依题意应有代入两个点的坐标得到求解。
,依题意应有代入两个点的坐标得到求解。
(2)椭圆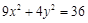 的焦点坐标为
的焦点坐标为 ,从而可设所求椭圆的方程为
,从而可设所求椭圆的方程为 ,然后经过点
,然后经过点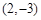 ,得方程的求解。
,得方程的求解。
解法1:①当所求椭圆的焦点在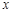 轴上时,设它的标准方程为
轴上时,设它的标准方程为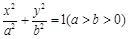 ,依题意应有,
,依题意应有,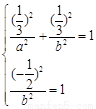 ,解得
,解得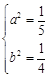 ,因为
,因为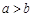 从而方程组无解;
从而方程组无解;
②当所求椭圆的焦点在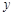 轴上时,设它的标准方程为
轴上时,设它的标准方程为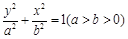 ,依题意应有
,依题意应有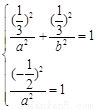 ,解得
,解得 ,所以所求椭圆的标准方程为
,所以所求椭圆的标准方程为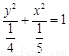 。
。
故所求椭圆的标准方程为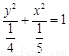 。
。
解法2:设所求椭圆的标准方程为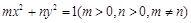 ,依题意得
,依题意得 ,解得
,解得 ,从而所求椭圆的标准方程为
,从而所求椭圆的标准方程为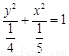 。
。
(2) ∵椭圆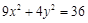 的焦点坐标为
的焦点坐标为 ,从而可设所求椭圆的方程为
,从而可设所求椭圆的方程为 ,又∵经过点
,又∵经过点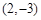 ,从而得
,从而得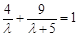 ,解得
,解得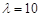 或
或 (舍去),
(舍去),
故所求椭圆的标准方程为 。
。

练习册系列答案
相关题目