题目内容
(1)抛物线的顶点在原点,焦点在射线x-y+1=0(x≥0)上求抛物线的标准方程;(2)求一条渐近线方程是3x+4y=0,一个焦点是(5,0)的双曲线标准方程,并求此双曲线的离心率.
【答案】分析:(1)利用焦点在射线x-y+1=0(x≥0)上,先求抛物线的焦点,再求抛物线的方程;
(2)根据双曲线一条渐近线方程是3x+4y=0,假设双曲线方程,利用焦点是(5,0),确定双曲线标准方程,从而可求此双曲线的离心率
解答:解:(1)由于抛物线的标准方程的焦点在坐标轴上
∴射线x-y+1=0(x≥0)与y轴交点(0,1)为抛物线的焦点,
∴抛物线方程为x2=4y.
(2)设双曲线方程为:9x2-16y2=λ,
∵双曲线有一个焦点为(4,0),∴λ>0
双曲线方程化为: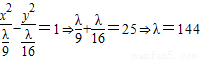 ,
,
∴双曲线方程为: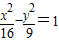
∴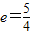 .
.
点评:本题重点考查抛物线的标准方程,考查双曲线的标准方程与离心率,解题的关键是求出抛物线、双曲线的标准方程,属于基础题.
(2)根据双曲线一条渐近线方程是3x+4y=0,假设双曲线方程,利用焦点是(5,0),确定双曲线标准方程,从而可求此双曲线的离心率
解答:解:(1)由于抛物线的标准方程的焦点在坐标轴上
∴射线x-y+1=0(x≥0)与y轴交点(0,1)为抛物线的焦点,
∴抛物线方程为x2=4y.
(2)设双曲线方程为:9x2-16y2=λ,
∵双曲线有一个焦点为(4,0),∴λ>0
双曲线方程化为:
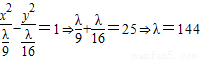 ,
,∴双曲线方程为:
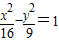
∴
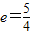 .
.点评:本题重点考查抛物线的标准方程,考查双曲线的标准方程与离心率,解题的关键是求出抛物线、双曲线的标准方程,属于基础题.

练习册系列答案
相关题目