Question

已知函数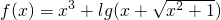，且x₁+x₂＞0，x₂+x₃＞0，x₃+x₁＞0，则f（x₁）+f（x₂）+f（x₃）的值

1. A.
   小于0
2. B.
   大于0
3. C.
   等于0
4. D.
   以上都有可能

Answer 1

B
分析：先判断奇偶性和单调性，先由单调性定义由自变量的关系得到函数关系，然后三式相加得解．
解答：易证f（x）是R上的奇函数与增函数．
∵x₁+x₂＞0，x₂+x₃＞0，x₃+x₁＞0
∴x₁＞-x₂，x₂＞-x₃，x₃＞-x₁，
∴f（x₁）＞f（-x₂），f（x₂）＞f（-x₃），f（x₃）＞f（-x₁）
∴f（x₁）+f（x₂）＞0，f（x₂）+f（x₃）＞0，f（x₃）+f（x₁）＞0，
三式相加得：
f（x₁）+f（x₂）+f（x₃）＞0
故选B．
点评：本题主要考查函数的奇偶性和单调性的定义，关键是通过变形转化到定义模型．