题目内容
设P是函数y=x+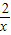
（x＞0）的图象上任意一点，过点P分别向直线y=x和y轴作垂线，垂足分别为A、B，则
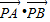的值是 ．
【答案】分析：设P（x，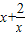
）（x＞0），可得|PA|，|PB|，由O、A、P、B四点共圆，可得∠APB=
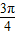，由数量积定义可求．
解答：解：设P（x，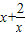
）（x＞0），则点P到直线y=x和y轴的距离分别为
|PA|=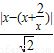
=
，|PB|=x．
∵O、A、P、B四点共圆，所以∠APB=π-∠AOB=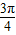
∴
=
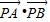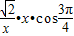=-1
故答案为：-1
点评：本题考查平面向量数量积的运算，涉及点到直线的距离公式和四点共圆的性质，属中档题．
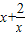）（x＞0），可得|PA|，|PB|，由O、A、P、B四点共圆，可得∠APB=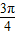，由数量积定义可求．解答：解：设P（x，
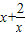）（x＞0），则点P到直线y=x和y轴的距离分别为|PA|=
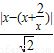=，|PB|=x．∵O、A、P、B四点共圆，所以∠APB=π-∠AOB=
∴
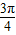
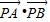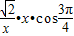==-1故答案为：-1
点评：本题考查平面向量数量积的运算，涉及点到直线的距离公式和四点共圆的性质，属中档题．
练习册系列答案
相关题目
（x＞0）的图象上任意一点，过点P分别向直线y=x和y轴作垂线，垂足分别为A、B，则
的值是________．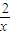
（x＞0）的图象上任意一点，过点P分别向直线y=x和y轴作垂线，垂足分别为A、B，则
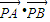的值是 ．