题目内容
函数f(x)=
,若f(a)>2,则实数a的取值范围是______.
|
当a≤0时,由f(a)>2可得,a
+3>2,解得-1<a≤0.
当a>0时,由f(a)>2可得 3a+1>2,解得 a>0.
综上可得,实数a的取值范围是 (-1,0]∪(0,+∞),
故答案为 (-1,0]∪(0,+∞).
| 1 |
| 3 |
当a>0时,由f(a)>2可得 3a+1>2,解得 a>0.
综上可得,实数a的取值范围是 (-1,0]∪(0,+∞),
故答案为 (-1,0]∪(0,+∞).

练习册系列答案
相关题目
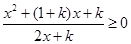 (
(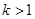 ).
).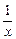 )>1
)>1 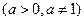
 的解集是 。
的解集是 。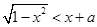 在区间
在区间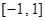 上恒成立,则实数
上恒成立,则实数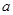 的取值范围是 .
的取值范围是 .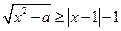 。
。 时,不等式
时,不等式 恒成立,则
恒成立,则 的取值范围是 ( )
的取值范围是 ( )