题目内容
解不等式loga(1-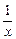 )>1
)>1 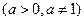
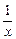 )>1
)>1 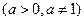
当a>1时,不等式的解集是{x| <x<0
<x<0 ,当0<a<1时,不等式的解集为{x|1<x<
,当0<a<1时,不等式的解集为{x|1<x< }.
}.
 <x<0
<x<0 ,当0<a<1时,不等式的解集为{x|1<x<
,当0<a<1时,不等式的解集为{x|1<x< }.
}.借助于单调性进行分类讨论
(1)当a>1时,原不等式等价于不等式组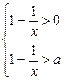
由此得1-a>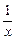 .因为1-a<0,所以x<0,∴
.因为1-a<0,所以x<0,∴ <x<0.
<x<0.
(2)当0<a<1时,原不等式等价于不等式组: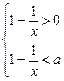
由①得x>1或x<0,由②得0 <x< ,∴1<x<
,∴1<x< .
.
综上,当a>1时,不等式的解集是{x| <x<0
<x<0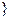 ,当0<a<1时,不等式的解集为{x|1<x<
,当0<a<1时,不等式的解集为{x|1<x< }.
}.
【名师指引】解指数不等式与对数不等式通常是由指数函数和对数函数的单调性转化为一般的不等式(组)来求解,当底数含参数时要进行分类讨论.

(1)当a>1时,原不等式等价于不等式组
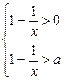
由此得1-a>
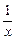 .因为1-a<0,所以x<0,∴
.因为1-a<0,所以x<0,∴ <x<0.
<x<0.(2)当0<a<1时,原不等式等价于不等式组:
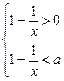
由①得x>1或x<0,由②得0 <x<
 ,∴1<x<
,∴1<x< .
.综上,当a>1时,不等式的解集是{x|
 <x<0
<x<0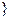 ,当0<a<1时,不等式的解集为{x|1<x<
,当0<a<1时,不等式的解集为{x|1<x< }.
}.【名师指引】解指数不等式与对数不等式通常是由指数函数和对数函数的单调性转化为一般的不等式(组)来求解,当底数含参数时要进行分类讨论.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
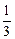 )
)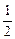 )
)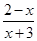 >0的解集为___________.
>0的解集为___________. 、
、 、
、 的大小关系是 ( )
的大小关系是 ( ) 



 其中a,b都大于0,请猜想若a,b都大于0,
其中a,b都大于0,请猜想若a,b都大于0, .
. 的解集为 。
的解集为 。 的解集是
的解集是 ,则
,则 的值为___________
的值为___________


 ,则函数
,则函数 的值域是( )
的值域是( )


