题目内容
已知A(0,2,3)、B(-2,1,6)、C(1,-1,5)为空间三点,(1)求以AB、AC为邻边的平行四边形的面积;
(2)若|a|=![]() ,且a分别与
,且a分别与![]() 、
、![]() 垂直,求向量a的坐标.
垂直,求向量a的坐标.
解析:(1)![]() =(-2,-1,3),
=(-2,-1,3),![]() =(1,-3,2),设
=(1,-3,2),设![]() 、
、![]() 的夹角为θ,
的夹角为θ,
则cosθ=![]() ,
,
∴sinθ=![]() .S
.S![]() ABCD=|
ABCD=|![]() ||
||![]() |sinθ=7
|sinθ=7![]() .
.
即以AB、AC为邻边的平行四边形的面积为7![]() .
.
(2)设a=(x,y,z),根据题意得a·![]() =(x,y,z)·(-2,-1,3)=-2x-y+3z=0, ①
=(x,y,z)·(-2,-1,3)=-2x-y+3z=0, ①
a·![]() =(x,y,z)·(1,-3,2)=x-3y+2z=0. ②
=(x,y,z)·(1,-3,2)=x-3y+2z=0. ②
又∵|a|=![]() ,∴
,∴![]() =
=![]() . ③
. ③
解由①②③组成的方程组,得x=1,y=1,z=1或x=-1,y=-1,z=-1.
∴a=(1,1,1)或(-1,-1,-1).

练习册系列答案
相关题目
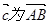 的位置向量,
的位置向量, 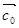 为
为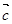 的单位向量,则单位向量
的单位向量,则单位向量