题目内容
北京的高考数学试卷共有8道选择题,每个选择题都给了4个选项(其中有且仅有一个是正确的).评分标准规定:每题只选1项,答对得5分,不答或答错得0分.某考生每道题都给出了答案,已确定有4道题的答案是正确的,而其余的题中,有两道题每题都可判断其两个选项是错误的,有一道题可以判断其一个选项是错误的,还有一道题因不理解题意只能乱猜.对于这8道选择题,试求:
(Ⅰ)该考生得分为40分的概率;
(Ⅱ)通过计算说明,该考生得多少分的可能性最大?
(Ⅰ)该考生得分为40分的概率;
(Ⅱ)通过计算说明,该考生得多少分的可能性最大?
分析:(Ⅰ)要得40分,8道选择题必须全做对,在其余四道题中,有两道题答对的概率为
,有一道题答对的概率为
,还有一道题答对的概率为
,由此能求出他做选择题得60分的概率.
(Ⅱ)依题意,该考生选择题得分的可能取值有:20,25,30,35,40共5种.得分为20表示只做对了四道题,其余各题都做错;类似的,能够求出得25分为的概率、得分为30的概率、得分为35的概率和得分为40的概率由此能得到最终结果.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
(Ⅱ)依题意,该考生选择题得分的可能取值有:20,25,30,35,40共5种.得分为20表示只做对了四道题,其余各题都做错;类似的,能够求出得25分为的概率、得分为30的概率、得分为35的概率和得分为40的概率由此能得到最终结果.
解答:解:(Ⅰ)要得40分,8道选择题必须全做对,在其余四道题中,有两道题答对的概率为
,
有一道题答对的概率为
,还有一道题答对的概率为
,
所以得40分的概率为P=
×
×
×
=
.
(Ⅱ)依题意,该考生得分的集合是{20,25,30,35,40},
得分为20表示只做对了四道题,其余各题都做错,所求概率为P1=
×
×
×
=
;
同样可求得得分为25分的概率为P2=
×
×
×
×
+
×
×
×
+
×
×
×
=
;
得分为30分的概率为P3=
;
得分为35分的概率为P4=
;
得分为40分的概率为P5=
所以得分为25分或30分的可能性最大.
| 1 |
| 2 |
有一道题答对的概率为
| 1 |
| 3 |
| 1 |
| 4 |
所以得40分的概率为P=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 48 |
(Ⅱ)依题意,该考生得分的集合是{20,25,30,35,40},
得分为20表示只做对了四道题,其余各题都做错,所求概率为P1=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 8 |
同样可求得得分为25分的概率为P2=
| C | 1 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
| 17 |
| 48 |
得分为30分的概率为P3=
| 17 |
| 48 |
得分为35分的概率为P4=
| 7 |
| 48 |
得分为40分的概率为P5=
| 1 |
| 48 |
所以得分为25分或30分的可能性最大.
点评:本题考查概率的性质和应用,解题时要认真审题,仔细解答,注意概念乘法公式的合理运用.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 的分布列及数学期望
的分布列及数学期望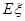 .
.