Question

设函数f（x）=x-[x]，其中[x]为取整记号，如[-1，2]=-2，[1，2]=1，[1]=1．又函数g（x）=-

x

3

，f（x）在区间（0，2）上零点的个数记为m，f（x）与g（x）图象交点的个数记为n，则

∫

n m

g（x）dx的值是（　　）

• A、-

  5

  2

• B、-

  4

  3

• C、-

  5

  4

• D、-

  7

  6

Answer 1

分析：由题意得：f（x）为周期函数，周期为1，x∈[0，1）时，f（x）=x．其图象如图所示．观察图象得m和n的值．最后利用定积分即可求得答案．

解答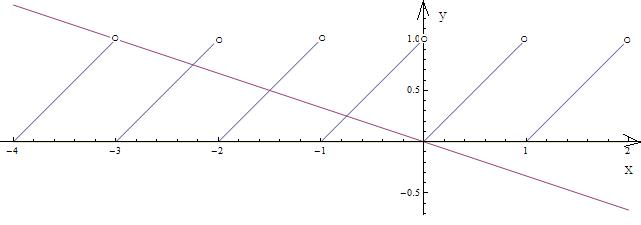：解：由题意得：
f（x）为周期函数，周期为1，x∈[0，1）时，f（x）=x．其图象如图所示．
观察图象得：
m=2，n=4．
则∫_mⁿg（x）dx=∫₂⁴（-

1

3

x）dx
=-（

1

6

x²）|₂⁴=-

5

2

．
故选A．

点评：本小题主要考查函数的零点、函数图象、函数与方程的综合运用等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．