题目内容
若函数f(x)=3sin(2x+φ)对任意x都有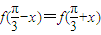 .
.(1)求
 的值.(2)求φ的最小正值.(3)函数f(x)的图象可由函数y=sinx的图象经过怎样的变换得到.
的值.(2)求φ的最小正值.(3)函数f(x)的图象可由函数y=sinx的图象经过怎样的变换得到.
【答案】分析:(1)根据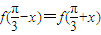 可知
可知 是f(x)的对称轴,进而可推断它在对称轴处有最大或最小值,进而求得
是f(x)的对称轴,进而可推断它在对称轴处有最大或最小值,进而求得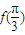 值.(2)把x=
值.(2)把x=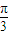 代入函数f(x),再根据
代入函数f(x),再根据 进而可求得φ.
进而可求得φ.
(3)根据函数图象的变换原则可知,函数f(x)的图象由函数y=sinx的图象向左平移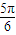 个单位,再将横坐标缩短到原来的
个单位,再将横坐标缩短到原来的 倍,把纵坐标伸长到原来3倍得到的.
倍,把纵坐标伸长到原来3倍得到的.
解答:解:(1)由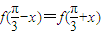 ,得
,得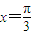 是f(x)的对称轴,它在对称轴处有最大或最小值,∴
是f(x)的对称轴,它在对称轴处有最大或最小值,∴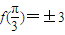 ;
;
(2)由(1)得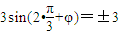 ,∴
,∴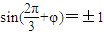 ,于是
,于是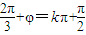 ,
,
∴ ,取k=1,得φ的最小正值为
,取k=1,得φ的最小正值为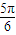 ;
;
(3)由(2)得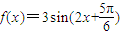 ,把函数y=sinx的图象向左平移
,把函数y=sinx的图象向左平移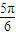 个单位,
个单位,
得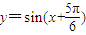 ,再将横坐标缩短到原来的
,再将横坐标缩短到原来的 倍得
倍得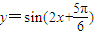 ,后把纵坐标伸长到原来3倍即得函数
,后把纵坐标伸长到原来3倍即得函数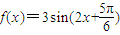 的图象
的图象
点评:本题主要考查函数y=Asin(ωx+φ)的图象变换和图象的性质.属基础题.
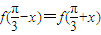 可知
可知 是f(x)的对称轴,进而可推断它在对称轴处有最大或最小值,进而求得
是f(x)的对称轴,进而可推断它在对称轴处有最大或最小值,进而求得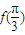 值.(2)把x=
值.(2)把x=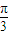 代入函数f(x),再根据
代入函数f(x),再根据 进而可求得φ.
进而可求得φ.(3)根据函数图象的变换原则可知,函数f(x)的图象由函数y=sinx的图象向左平移
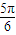 个单位,再将横坐标缩短到原来的
个单位,再将横坐标缩短到原来的 倍,把纵坐标伸长到原来3倍得到的.
倍,把纵坐标伸长到原来3倍得到的.解答:解:(1)由
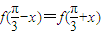 ,得
,得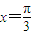 是f(x)的对称轴,它在对称轴处有最大或最小值,∴
是f(x)的对称轴,它在对称轴处有最大或最小值,∴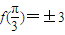 ;
;(2)由(1)得
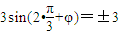 ,∴
,∴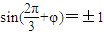 ,于是
,于是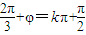 ,
,∴
 ,取k=1,得φ的最小正值为
,取k=1,得φ的最小正值为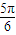 ;
;(3)由(2)得
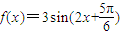 ,把函数y=sinx的图象向左平移
,把函数y=sinx的图象向左平移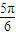 个单位,
个单位,得
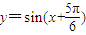 ,再将横坐标缩短到原来的
,再将横坐标缩短到原来的 倍得
倍得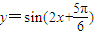 ,后把纵坐标伸长到原来3倍即得函数
,后把纵坐标伸长到原来3倍即得函数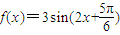 的图象
的图象点评:本题主要考查函数y=Asin(ωx+φ)的图象变换和图象的性质.属基础题.

练习册系列答案
相关题目
 如图,M是单位圆与x轴正半轴的交点,点P在单位圆上,
如图,M是单位圆与x轴正半轴的交点,点P在单位圆上, 如图,M是单位圆与x轴正半轴的交点,点P在单位圆上,
如图,M是单位圆与x轴正半轴的交点,点P在单位圆上,