题目内容
 如图,M是单位圆与x轴正半轴的交点,点P在单位圆上,∠MOP=x(0<x<π),
如图,M是单位圆与x轴正半轴的交点,点P在单位圆上,∠MOP=x(0<x<π),| OQ |
| OM |
| OP |
| OM |
| OQ |
| 3 |
(1)求函数f(x)的表达式及单调递增区间;
(2)在△ABC中,a、b、c分别为角A、B、C的对边,若f(A)=3,a=2
| 3 |
分析:(1)由题设条件知M(1,0),P(cosx,sinx),故
=(1+cosx,sinx),
•
=1+cosx,S=sinx,由此能求出函数f(x)的表达式及单调递增区间;
(2)根据f(A)=3可求出A,然后利用正弦定理求出角B,最后根据勾股定理可求出c的值.
| PQ |
| OM |
| OQ |
(2)根据f(A)=3可求出A,然后利用正弦定理求出角B,最后根据勾股定理可求出c的值.
解答:解:(1)∵点M是单位圆O(O是坐标原点)与X轴正半轴的交点,
∴M(1,0),
∵点P在单位圆上,∠MOP=x,OQ=OP=OM,
∴P(cosx,sinx),
∴
=(1+cosx,sinx),
•
=1+cosx,
∵S=sinx,
∴f(x)=1+cosx+
sinx=2sin(x+
)+1,0<x<π,
令-
+2kπ≤x+
≤
+2kπ,
∴-
+2kπ≤x≤
+2kπ,k∈Z.
∵0<x<π,
∴函数f(x)的单递增调区间为(0,
].
(2)∵f(A)=3∴2sin(A+
)+1=3∴sin(A+
)=1
在△ABC中,0<A<π,
<A+
<
,
∴A+
=
,A=
由a=2
,b=2及正弦定理得
=
即
=
∴sinB=
∵0<B<π,B<A∴B=
∴C=
∴c2=a2+b2=16
∴c=4

∴M(1,0),
∵点P在单位圆上,∠MOP=x,OQ=OP=OM,
∴P(cosx,sinx),
∴
| PQ |
| OM |
| OQ |
∵S=sinx,
∴f(x)=1+cosx+
| 3 |
| π |
| 6 |
令-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴-
| 2π |
| 3 |
| π |
| 3 |
∵0<x<π,
∴函数f(x)的单递增调区间为(0,
| π |
| 3 |
(2)∵f(A)=3∴2sin(A+
| π |
| 6 |
| π |
| 6 |
在△ABC中,0<A<π,
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴A+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
由a=2
| 3 |
| a |
| sinA |
| b |
| sinB |
即
2
| ||
sin
|
| 2 |
| sinB |
| 1 |
| 2 |
∵0<B<π,B<A∴B=
| π |
| 6 |
| π |
| 2 |
∴c2=a2+b2=16
∴c=4
点评:本题主要考查了函数单调递增区间,以及正弦定理,注意单位圆及三角函数知识的合理运用,同时考查了运算求解的能力,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 如图,M是单位圆与x轴正半轴的交点,点P在单位圆上,
如图,M是单位圆与x轴正半轴的交点,点P在单位圆上,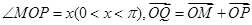 ,四边形OMQP的面积为S,函数
,四边形OMQP的面积为S,函数
 的表达式及单调递增区间;
的表达式及单调递增区间; 中,a、b、c分别为角A、B、C的对边,若
中,a、b、c分别为角A、B、C的对边,若 ,求a的值。
,求a的值。
 ,四边形OMQP的面积为S,函数
,四边形OMQP的面积为S,函数 .
. ,求c的值.
,求c的值.
 ,四边形OMQP的面积为S,函数
,四边形OMQP的面积为S,函数 .
. ,求c的值.
,求c的值.