Question

（本小题满分12分）函数f(x)对任意的a、b∈R,都有f(a+b)=f(a)+ f(b)-1,并且

当x＞0时，f(x)＞1.

（1）求证：f(x)是R上的增函数；

（2）若f(4)=5,解不等式f(3m²-m-2)＜3.

 

Answer 1

【答案】

（1）略

（2）-1＜m＜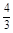

【解析】解  （1）设x₁,x₂∈R，且x₁＜x₂,

则x₂- x₁＞0,∴f(x₂- x₁)＞1.            2分

f(x₂)-f(x₁)=f((x₂- x₁)+ x₁)-f(x₁)

=f(x₂- x₁)+f(x₁)-1-f(x₁)=f(x₂- x₁)-1＞0.   5分

∴f（x₂）＞f(x₁).

即f(x)是R上的增函数.                       6分

（2）∵f（4）=f（2+2）=f（2）+f（2）-1=5，

∴f（2）=3，                          8分

∴原不等式可化为f(3m²-m-2)＜f(2),

∵f(x)是R上的增函数，∴3m²-m-2＜2,            10分

解得-1＜m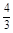＜,故解集为（-1,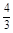）.                       12分