题目内容
若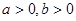
，且函数
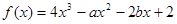在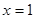
处有极值，则ab的最大值为 ．
9
解析试题分析：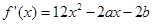
，∵f(x)在x=1处取极值，∴
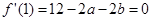，即a+b=6，根据基本不等式
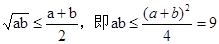，∴ab的最小值为9.
考点：导数的运用，基本不等式求最值.
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
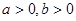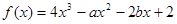若，且函数在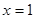处有极值，则ab的最大值为 ．
9
解析试题分析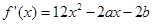：，∵f(x)在x=1处取极值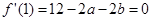，∴，即a+b=6，根据基本不等式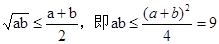，∴ab的最小值为9.
考点：导数的运用，基本不等式求最值.
阅读快车系列答案
的导函数为
，若对于定义域内任意
，
，有
恒成立，则称
；②
；③
；④
；⑤
．其中为恒均变函数的序号是 ．（写出所有满足条件的函数的序号）
都有对称中心．请你探究函数
,猜想它的对称中心为_________．
上点
处的切线平行于直线
，则点
在点
处的切线斜率为 ．
4)f(
f(
)f(lg
＝φ′(x)·ln f(x)＋φ(x)·
，于是y′＝f(x)φ(x)[φ′(x)·ln f(x)＋φ(x)·
的单调递增区间是________．