题目内容
本题满分14分)
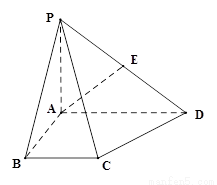
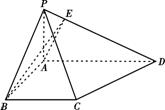
四棱锥P-ABCD中,底面ABCD为直角梯形, ,AD∥BC, AB=BC=2, AD=4,
,AD∥BC, AB=BC=2, AD=4,
PA⊥底面ABCD,PD与底面ABCD成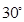 角,E是PD的中点.
角,E是PD的中点.
(1) 点H在AC上且EH⊥AC,求 的坐标;
的坐标;
(2) 求AE与平面PCD所成角的余弦值;
【答案】
(1)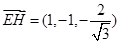 ;(2)
;(2)
【解析】第一问以AB,AD,AP分别为x,y,z轴,建立如图所示的坐标系。
则由条件知,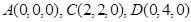
而:PA⊥底面ABCD,PD与底面ABCD成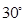 角
角
∴ , ∴
, ∴ ∴
∴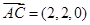
设 , ∴
, ∴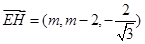
由EH⊥AC得,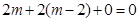 ,解得
,解得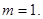
第二问由上得, 而
而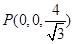 ,
,
∴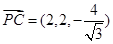 ,
,

记平面PCD的一个法向量为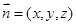 ,则
,则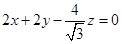 且
且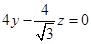
解得 取
取
则
解(1) 以AB,AD,AP分别为x,y,z轴,建立如图所示的坐标系。
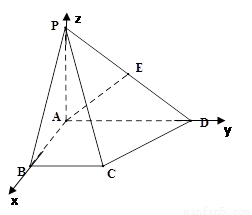
则由条件知,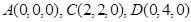 ---------------2分
---------------2分
而:PA⊥底面ABCD,PD与底面ABCD成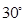 角
角
∴ , ∴
, ∴ --------------4分
--------------4分
∴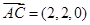
设 , ∴
, ∴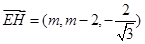
由EH⊥AC得,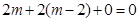 ,解得
,解得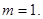 --------------6分
--------------6分
∴所求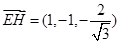 --------------7分
--------------7分
(2)由上得, 而
而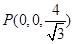 ,
,
∴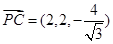 ,
,  --------------9分
--------------9分
记平面PCD的一个法向量为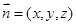 ,则
,则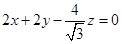 且
且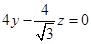
解得 取
取 --------------11分
--------------11分
则 ,
--------------13分
,
--------------13分
设AE与平面PCD所成角为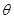 ,则
,则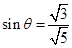 ,则所求的余弦值为
,则所求的余弦值为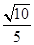 --------------14分
--------------14分

练习册系列答案
相关题目
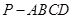 的底面
的底面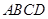 为矩形,且
为矩形,且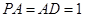 ,
,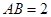 ,
,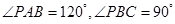 ,
,
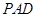 与平面
与平面 是否垂直?并说明理由;
是否垂直?并说明理由;  与平面
与平面 中,底面
中,底面 为矩形,平面
为矩形,平面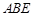 ,
,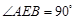 ,
,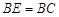 ,
,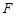 为
为 的中点,
的中点,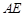 ∥平面
∥平面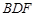 ;(2)平面
;(2)平面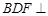 平面
平面 .
.
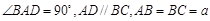 ,
,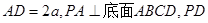 与底面成30°角.
与底面成30°角. 为垂足,求证:
为垂足,求证: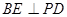 ;
;
 ,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.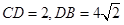 ,求四棱锥F-ABCD的体积.
,求四棱锥F-ABCD的体积.