题目内容
设x是任意的一个实数，y表示对x进行四舍五入后的结果，其实质是取与x最接近的整数，在距离相同时，取较大的而不取较小的整数，其函数关系常用y=round（x）表示．例如：round（0.5）=1，round（2.48）=2，round（-0.49）=0，round（-2.51）=-3．
（1）画出这个函数y=round（x）在区间[-5，5]内的函数图象；
（2）判断函数y=round（x）（x∈R）的奇偶性，并说明理由；
（3）求方程round（2x+1）=4x的解集．
解：（1）见图；（2）非奇非偶函数．
因为round（-0.5）=0，round（0.5）=1
所以round（-0.5）≠round（0.5），round（-0.5）≠-round（0.5）
故函数为既非奇又非偶函数．
（3）原不等式
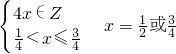
所以，方程的解集为
．分析：（1）图象如图所示．
（2）是非奇非偶函数．因为round（-0.5）=0，round（0.5）=1，显然round（-0.5）≠round（0.5），且round（-0.5）≠-round（0.5）．
（3）原不等式
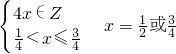，由此可得方程的解．点评：本题主要考查新定义，函数的奇偶性的判断，作函数的图象，属于中档题．
练习册系列答案
相关题目
设x是任意的一个实数，y表示对x进行四舍五入后的结果，其实质是取与x最接近的整数，在距离相同时，取较大的而不取较小的整数，其函数关系常用y=round（x）表示．例如：round（0.5）=1，round（2.48）=2，round（-0.49）=0，round（-2.51）=-3．
