题目内容
某学校为了解高三年级学生寒假期间的学习情况,抽取甲、乙两班,调查这两个班的学生在寒假期间每天平均学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生每天平均学习时间在区间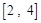 的有8人.
的有8人.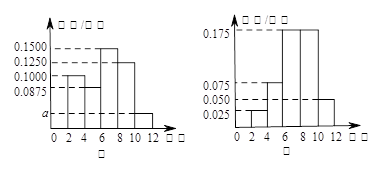
(1)求直方图中 的值及甲班学生每天平均学习时间在区间
的值及甲班学生每天平均学习时间在区间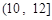 的人数;
的人数;
(2)从甲、乙两个班每天平均学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(1) ;3(2)详见解析
;3(2)详见解析
解析试题分析:(1)频率分布直方图中每个小矩形的面积表示概率,概率和为1,则可求得 。因为甲班学生每天平均学习时间在区间
。因为甲班学生每天平均学习时间在区间 的有8人,根据公式
的有8人,根据公式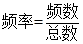 可求得甲班学生总数,再根据
可求得甲班学生总数,再根据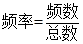 可得甲班学生每天平均学习时间在区间
可得甲班学生每天平均学习时间在区间 的人数。(2)乙两个班每天平均学习时间大于10个小时的学生仍用公式
的人数。(2)乙两个班每天平均学习时间大于10个小时的学生仍用公式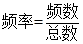 可求得为4人。
可求得为4人。 的可能取值为0、1、2、3.根据古典概型概率公式
的可能取值为0、1、2、3.根据古典概型概率公式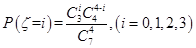 可得
可得 各取值时的概率,从而可得其分布列,再根据期望公式可求其期望值。
各取值时的概率,从而可得其分布列,再根据期望公式可求其期望值。
解:⑴ 由直方图知, ,解得
,解得 ,
,
因为甲班学习时间在区间 的有8人,
的有8人,
所以甲班的学生人数为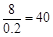 ,
,
所以甲、乙两班人数均为40人.所以甲班学习时间在区间 的人数为
的人数为 (人).
(人).
⑵ 乙班学习时间在区间 的人数为
的人数为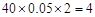 (人).
(人).
由⑴知甲班学习时间在区间 的人数为3人,
的人数为3人,
在两班中学习时间大于10小时的同学共7人, 的所有可能取值为0,1,2,3.
的所有可能取值为0,1,2,3. ,
, ,
, ,
, .
.
所以随机变量 的分布列为:
的分布列为:
 .
.
考点:1频率分布直方图;2古典概型概率公式;3分布列及期望。

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案甲、乙二人参加知识竞答,共有10个不同的题目,其中选择题6个,判断题4个,甲、乙二人依次各抽一题,那么
(1)甲抽到选择题,乙抽到判断题的概率是多少?
(2)甲、乙二人中至少有一个抽到选择题的概率是多少?
某大型公益活动从一所名牌大学的四个学院中选出了 名学生作为志愿者,参加相关的活
名学生作为志愿者,参加相关的活
动事宜.学生来源人数如下表:
| 学院 | 外语学院 | 生命科学学院 | 化工学院 | 艺术学院 |
| 人数 |  |  |  | 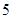 |
(1)若从这
 名学生中随机选出两名,求两名学生来自同一学院的概率;
名学生中随机选出两名,求两名学生来自同一学院的概率;(2)现要从这
 名学生中随机选出两名学生向观众宣讲此次公益活动的主题.设其中来自外语学院的人数为
名学生中随机选出两名学生向观众宣讲此次公益活动的主题.设其中来自外语学院的人数为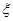 ,令
,令 ,求随机变量
,求随机变量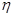 的分布列及数学期望
的分布列及数学期望 .
. 
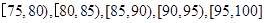 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2. 的一次函数
的一次函数
 和
和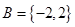 ,分别从集合
,分别从集合 和
和 中随机取一个数作为
中随机取一个数作为 ,
, ,求函数
,求函数 ,求函数
,求函数