题目内容
已知关于 的一次函数
的一次函数
(1)设集合 和
和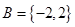 ,分别从集合
,分别从集合 和
和 中随机取一个数作为
中随机取一个数作为 ,
, ,求函数
,求函数 是增函数的概率;
是增函数的概率;
(2)若实数 ,
, 满足条件
满足条件 ,求函数
,求函数 的图象不经过第四象限的概率.
的图象不经过第四象限的概率.
(1)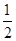 ;(2)
;(2)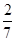
解析试题分析:(1)依题意,基本事件总数为8个,记“函数 是增函数”为事件A,则
是增函数”为事件A,则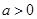 ,事件A包含的基本事件分别为:
,事件A包含的基本事件分别为: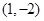 ,
,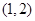 ,
, ,
,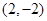 ,共4个,由古典概型的概率计算公式得,所求概率为
,共4个,由古典概型的概率计算公式得,所求概率为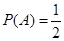 ;(2)本题还有两个变量,基本事件用有序实数对
;(2)本题还有两个变量,基本事件用有序实数对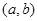 表示,画出不等式表示的平面区域,即基本事件空间,因为函数
表示,画出不等式表示的平面区域,即基本事件空间,因为函数 的图象不经过第四象限,则满足
的图象不经过第四象限,则满足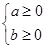 ,由几何概型的概率计算公式,可计算其面积的比即为概率.
,由几何概型的概率计算公式,可计算其面积的比即为概率.
试题解析:(1)抽取全部结果所构成的基本事件空间为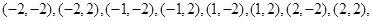 共8个4分
共8个4分
设函数是增函数为事件 ,
,
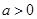 ,有4个
,有4个
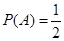 7分
7分
(2)实数 ,
, 满足条件
满足条件 ,要函数
,要函数 的图象不经过第四象限
的图象不经过第四象限
则需使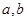 满足
满足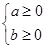 ,即
,即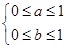 , 10分
, 10分
设“函数 的图象不经过第四象限”为事件B,则
的图象不经过第四象限”为事件B,则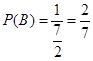 .
.
考点:1、一次函数的图象;2、古典概型;3、几何概型.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
如图,A地到火车站共有两条路径L1和L2,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
| 时间(分钟) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| L1的频率 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
| L2的频率 | 0 | 0.1 | 0.4 | 0.4 | 0.1 |
(1)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(2)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针地(1)的选择方案,求X的分布列和数学期望.
为了解心肺疾病是否与年龄相关,现随机抽取了40名市民,得到数据如下表:
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 大于40岁 | 16 | | |
| 小于等于40岁 | | 12 | |
| 合计 | | | 40 |
(1)请将
 列联表补充完整;
列联表补充完整;(2)已知大于40岁患心肺疾病市民中,经检查其中有4名重症患者,专家建议重症患者住院治疗,现从这16名患者中选出两名,记需住院治疗的人数为
 ,求
,求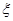 的分布列和数学期望;
的分布列和数学期望;(3)能否在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关?
下面的临界值表供参考:
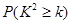 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
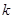 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
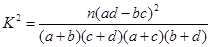 ,其中
,其中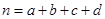 )
) 某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查.调查问卷共10道题,答题情况如下表:
| 答对题目数 |  | 8 | 9 |  |
| 女 | 2 | 13 | 12 | 8 |
| 男 | 3 | 37 | 16 | 9 |
(2)从答对题目数少于8的出租车司机中任选出两人做进一步的调查,求选出的两人中至少有一名女出租车司机的概率.
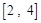 的有8人.
的有8人.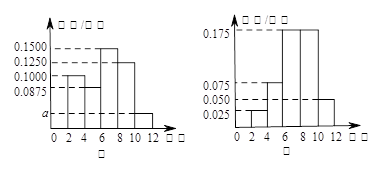
 的值及甲班学生每天平均学习时间在区间
的值及甲班学生每天平均学习时间在区间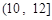 的人数;
的人数; ,求
,求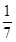 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数. ,乙组能使生物成活的概率为
,乙组能使生物成活的概率为 ,假定试验后生物成活,则称该试验成功,如果生物不成活,则称该次试验是失败的.
,假定试验后生物成活,则称该试验成功,如果生物不成活,则称该次试验是失败的. ,求
,求