题目内容
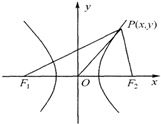
已知点P是双曲线C: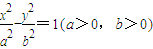 左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )
左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )
A.
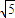
B.2
C.
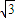
D.
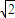
【答案】分析:在三角形F1F2P中,点N恰好平分线段PF2,点O恰好平分线段F1F2,根据三角形的中位线定理得出ON∥PF1,从而得到∠PF1F2正切值,可设PF2=bt.PF1=at,再根据双曲线的定义可知|PF2|-|PF1|=2a,进而根据勾股定理建立等式求得a和b的关系,则离心率可得.
解答:解:在三角形F1F2P中,点N恰好平分线段PF2,点O恰好平分线段F1F2,
∴ON∥PF1,又ON的斜率为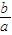 ,
,
∴tan∠PF1F2= ,
,
在三角形F1F2P中,设PF2=bt.PF1=at,
根据双曲线的定义可知|PF2|-|PF1|=2a,∴bt-at=2a,①
在直角三角形F1F2P中,|PF2|2+|PF1|2=4c2,∴b2t2+a2t2=4c2,②
由①②消去t,得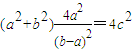 ,
,
又c2=a2+b2,
∴a2=(b-a)2,即b=2a,
∴双曲线的离心率是 =
=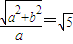 ,
,
故选A.
点评:本题主要考查了双曲线的简单性质,考查了学生对双曲线定义和基本知识的掌握,属于基础题.
解答:解:在三角形F1F2P中,点N恰好平分线段PF2,点O恰好平分线段F1F2,
∴ON∥PF1,又ON的斜率为
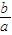 ,
,∴tan∠PF1F2=
 ,
,在三角形F1F2P中,设PF2=bt.PF1=at,
根据双曲线的定义可知|PF2|-|PF1|=2a,∴bt-at=2a,①
在直角三角形F1F2P中,|PF2|2+|PF1|2=4c2,∴b2t2+a2t2=4c2,②
由①②消去t,得
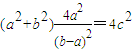 ,
,又c2=a2+b2,
∴a2=(b-a)2,即b=2a,
∴双曲线的离心率是
 =
=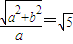 ,
,故选A.
点评:本题主要考查了双曲线的简单性质,考查了学生对双曲线定义和基本知识的掌握,属于基础题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 已知点P是双曲线C:
已知点P是双曲线C:| x2 |
| 8 |
| y2 |
| 4 |
| |PF1|+|PF2| |
| |OP| |
| A、[0,6] | ||||||
B、(2,
| ||||||
C、(
| ||||||
D、[0,
|
 (2013•婺城区模拟)已知点P是双曲线C:
(2013•婺城区模拟)已知点P是双曲线C: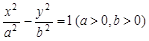 左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )
左支上一点,F1,F2是双曲线的左、右两个焦点,且PF1⊥PF2,PF2与两条渐近线相交于M,N两点(如图),点N恰好平分线段PF2,则双曲线的离心率是( )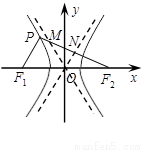
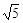 B.2 C.
B.2 C.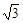 D.
D.