题目内容
(13分)已知数列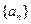 的前
的前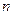 项和为
项和为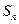 ,且
,且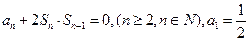 .
.
(1) 求证: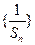 为等差数列; (2)求
为等差数列; (2)求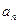 ; (3)若
; (3)若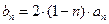 , 求
, 求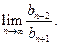
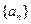 的前
的前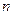 项和为
项和为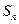 ,且
,且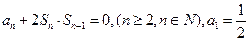 .
.(1) 求证:
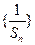 为等差数列; (2)求
为等差数列; (2)求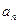 ; (3)若
; (3)若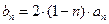 , 求
, 求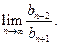
(Ⅰ)略 (Ⅱ) 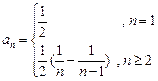 (Ⅲ)1
(Ⅲ)1
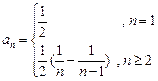 (Ⅲ)1
(Ⅲ)1:(1)当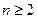 时,由已知有
时,由已知有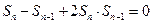 易知
易知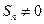
故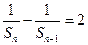 ∴
∴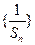 为首项为2,公差为2的等差数列.
为首项为2,公差为2的等差数列.
(2)易知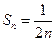 ,当
,当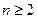 时,
时,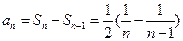 ∴
∴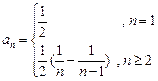
(3)易知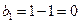 ,
,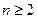 时
时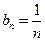 . ∴
. ∴
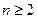 时,由已知有
时,由已知有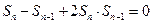 易知
易知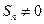
故
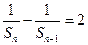 ∴
∴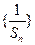 为首项为2,公差为2的等差数列.
为首项为2,公差为2的等差数列.(2)易知
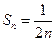 ,当
,当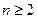 时,
时,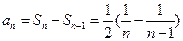 ∴
∴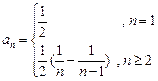
(3)易知
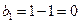 ,
,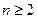 时
时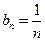 . ∴
. ∴

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
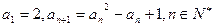
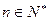 恒有
恒有 成立。
成立。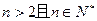 ,有
,有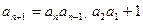 成立。
成立。 。
。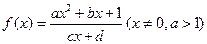 ,且当
,且当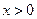 时,
时,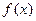 有最小值
有最小值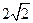 ,又
,又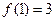 .(1)求
.(1)求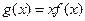 ,正数数列
,正数数列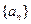 中,
中,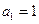 ,
,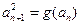 ,求数列
,求数列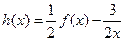 ,数列
,数列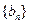 中
中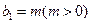 ,
,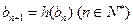 .是否存在常数
.是否存在常数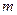 使
使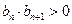 对任意
对任意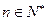 恒成立.若存在,求
恒成立.若存在,求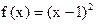 ,
,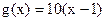 ,数列
,数列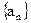 满足
满足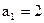 ,
,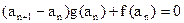 ,
,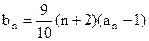 .
.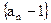 是等比数列;
是等比数列;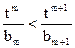 对任意
对任意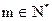 恒成立,求实数
恒成立,求实数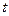 的取值范围.
的取值范围.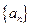 满足
满足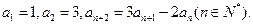
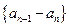 是等比数列; (II)求数列
是等比数列; (II)求数列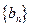 满足
满足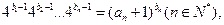 证明
证明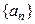 满足
满足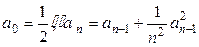 其中n=1,2,3,….
其中n=1,2,3,….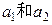 的值;
的值;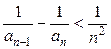 ;
;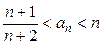 .
.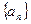 中,
中,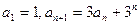 ,求数列
,求数列