Question

在同一平面直角坐标系中，画出三个函数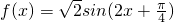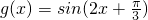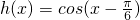，，的部分图象（如图），则

1. A.
   a为f（x），b为g（x），c为h（x）
2. B.
   a为h（x），b为f（x），c为g（x）
3. C.
   a为g（x），b为f（x），c为h（x）
4. D.
   a为h（x），b为g（x），c为f（x）

Answer 1

B
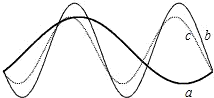
分析：从振幅、最小正周期的大小入手：b的振幅最大，故b为f（x）；a的最小正周期最大，故a为h（x），从而c为g（x）．
解答：由函数的图象可知图象b的振幅最高，结合解析式可知b为f（x）；由函数的图象可知图象a的最小正周期最小，结合解析式可知a为h（x）；从而可知c为g（x）．
故选B
点评：本题主要考查了利用三角函数的性质：三角函数的振幅、最小正周期等来判断函数的图象，考查了识图的能力．