题目内容
若实数 满足
满足 ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
C
解析试题分析:因为根据实数 满足
满足 ,作出可行域,可知那么区域内的点到原点的距离为
,作出可行域,可知那么区域内的点到原点的距离为 ,则求解
,则求解 的最小值,即为求解原点到(x,y)的距离的平方的最小值,直接做原点到直线x-y+1=0的垂线段即为距离的最小值,d=
的最小值,即为求解原点到(x,y)的距离的平方的最小值,直接做原点到直线x-y+1=0的垂线段即为距离的最小值,d= ,因此
,因此 的最小值
的最小值 ,选C.
,选C.
考点:本试题主要考查了不等式组表示的平面区域内点到原点距离的最值问题。
点评:易错点是忘记了平方得到的距离的最小值。解决该试题的关键是理解目标函数表示的几何意义就是两点之间的距离的平方最小值问题。

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
设 满足约束条件
满足约束条件 ,则
,则 的最大值为( )
的最大值为( )
| A.5 | B.7 | C.3 | D.-8 |
已知变量 满足
满足 ,目标函数是
,目标函数是 ,则有( )
,则有( )
A. | B.  无最小值 无最小值 |
C. 无最大值 无最大值 | D. 既无最大值,也无最小值 既无最大值,也无最小值 |
已知点 在不等式组
在不等式组 确定的平面区域内,则点
确定的平面区域内,则点 所在平面区域的面积是( )
所在平面区域的面积是( )
A. | B. | C. | D. |
当不等式组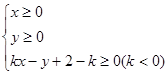 所表示的平面区域的面积最小时,实数k的值为( )
所表示的平面区域的面积最小时,实数k的值为( )
A.-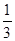 | B.-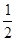 | C.-1 | D.-2 |
若实数 满足
满足 则
则 的最大值是
的最大值是
| A.0 | B.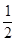 | C. 2 | D.3 |
若实数 ,
, 满足不等式组
满足不等式组 且
且 的最大值为9,则实数
的最大值为9,则实数
( )
A. | B.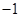 | C.1 | D. 2 |
不等式3x-2y-6>0表示的区域在直线3x-2y-6=0 的 ( )
| A.右上方 | B.右下方 | C.左上方 | D.左下方 |
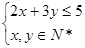 B.
B.
 D.
D.