题目内容
设
满足约束条件
,则
的最大值为（ ）
| A．5 | B．7 | C．3 | D．-8 |
B
解析试题分析：如图，作出可行域，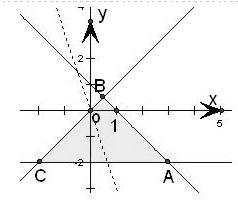
作出直线l0：y=-3x，将l0平移至过点A（3，-2）处时，函数z=3x+y有最大值7．
故选B
考点：本试题主要考查了线性规划问题，考查数形结合思想．
点评：解答的步骤是有两种方法：一种是：画出可行域画法，标明函数几何意义，得出最优解．另一种方法是：由约束条件画出可行域，求出可行域各个角点的坐标，将坐标逐一代入目标函数，验证，求出最优解．
练习册系列答案
相关题目
设变量x，y满足约束条件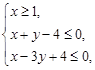
则目标函数z＝3x－y的最大值为
A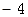． | B．0 | C． | D．4 |
动点
在区域
上运动，则
的范围（ ）。
A． | B． |
C． | D． |
下面给出的四个点中，位于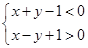
表示的平面区域内的点是（ ）
A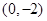． | B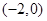． | C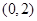． | D． |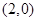
设变量
满足约束条件
，则目标函数
的最大值为（ ）
A． | B． | C． | D． |
已知实数对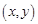
满足不等式组
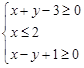，二元函数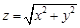
的最大值为（ ）
A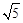． | B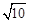． | C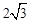． | D． |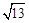
若直线y=2x上存在点（x，y）满足
则实数m的最大值为 ( )
| A．-1 | B．1 | C． | D．2 |
若实数
满足
，则
的最小值为（ ）
A． | B． | C． | D． |
某加工厂用某原料由甲车间加工出A产品,由乙车间加工出B产品.甲车间加工一箱原料需耗费工时10小时可加工出7千克A产品,每千克A产品获利40元.乙车间加工一箱原料需耗费工时6小时可加工出4千克B产品,每千克B产品获利50元.甲、乙两车间每天共能完成至多70箱原料的加工,每天甲、乙车间耗费工时总和不得超过480小时,甲、乙两车间每天总获利最大的生产计划为 ( )
| A．甲车间加工原料10箱,乙车间加工原料60箱 |
| B．甲车间加工原料15箱,乙车间加工原料55箱 |
| C．甲车间加工原料18箱,乙车间加工原料50箱 |
| D．甲车间加工原料40箱,乙车间加工原料30箱 |