题目内容
如果Sn=1+2+…+n(n∈N*),Tn=
×
×…×
(n≥2,n∈N*),则下列各数中与T2010最接近的数是( )
| S2 |
| S2-1 |
| S3 |
| S3-1 |
| Sn |
| Sn-1 |
| A、2.9 | B、3.0 |
| C、3.1 | D、3.2 |
分析:先利用等差数列的求和公式求出Sn=
,代入Tn=
×
×… ×
,整理可得T2010=
,算出其近视值.
| n(n+1) |
| 2 |
| S2 |
| S2-1 |
| S3 |
| S3-1 |
| Sn |
| Sn-1 |
| 3×2010 |
| 2012 |
解答:解:∵Sn=1+2+…+n=
∴Tn=
×
×…×
∴T2010=
×
×…×
=
×
×
×…×
=
=
≈2.997
故选 B
| n(n+1) |
| 2 |
∴Tn=
| S2 |
| S2-1 |
| S3 |
| S3-1 |
| Sn |
| Sn-1 |
∴T2010=
| S2 |
| S2-1 |
| S3 |
| S3-1 |
| S2010 |
| S2010- 1 |
=
| 2×3 |
| 1×4 |
| 3×4 |
| 2×5 |
| 4×5 |
| 3×6 |
| 2010×2011 |
| 2009×2012 |
=
| (2×3×4×…×2010)×(3×4×…×2011) |
| (1×2×3×…×2009)×(4×5×…×2012) |
=
| 3×2010 |
| 2012 |
故选 B
点评:本题以等差数列的和公式为载体考查相消法求出Tn,在求Tn=
×
× …×
要注意利用分组求积相消的技巧.
| 2×3 |
| 1×4 |
| 3×4 |
| 2×5 |
| 2010×2011 |
| 2009×2012 |

练习册系列答案
相关题目
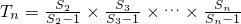 (n≥2,n∈N*),则下列各数中与T2010最接近的数是
(n≥2,n∈N*),则下列各数中与T2010最接近的数是 (n≥2,n∈N*),则下列各数中与T2010最接近的数是( )
(n≥2,n∈N*),则下列各数中与T2010最接近的数是( )