题目内容
大家知道,在数列{an}中,若an=n,则sn=1+2+3+…+n=
n2+
n,若an=n2,则
sn=12+22+32+…+n2=
n3+
n2+
n,于是,猜想:若an=n3,则sn=13+23+33+…+n3=an4+bn3+cn2+dn.
问:(1)这种猜想,你认为正确吗?
(2)不管猜想是否正确,这个结论是通过什么推理方法得到的?
(3)如果结论正确,请用数学归纳法给予证明.
| 1 |
| 2 |
| 1 |
| 2 |
sn=12+22+32+…+n2=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
问:(1)这种猜想,你认为正确吗?
(2)不管猜想是否正确,这个结论是通过什么推理方法得到的?
(3)如果结论正确,请用数学归纳法给予证明.
分析:(1)猜想正确;
(2)这是一种类比推理的方法;
(3)由类比可猜想,sn=13+23+33+…+n3=
n4+
n3+
n2,再用数学归纳法证明,关键注意n=k+1时的证明,要利用n=k时的结论.
(2)这是一种类比推理的方法;
(3)由类比可猜想,sn=13+23+33+…+n3=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:解:(1)猜想正确;
(2)这是一种类比推理的方法;
(3)由类比可猜想,a=
,n=1时,a+b+c+d=1;n=2时,16a+8b+4c+d=9;n=3时,81a+27b+9c+d=36
故解得a=
,b=
,c=
,∴sn=13+23+33+…+n3=
n4+
n3+
n2
用数学归纳法证明:
①n=1时,结论成立;
②假设n=k时,结论成立,即13+23+33+…+k3=
k4+
k3+
k2=[
]2
则n=k+1时,左边=13+23+33+…+k3+(k+1)3
=
k4+
k3+
k2+(k+1)3
=[
]2+(k+1)3
=(
)2(k2+4k+4)
=[
]2
=右边,结论成立
由①②可知,sn=13+23+33+…+n3=
n4+
n3+
n2,成立
(2)这是一种类比推理的方法;
(3)由类比可猜想,a=
| 1 |
| 4 |
故解得a=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
用数学归纳法证明:
①n=1时,结论成立;
②假设n=k时,结论成立,即13+23+33+…+k3=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| k(k+1) |
| 2 |
则n=k+1时,左边=13+23+33+…+k3+(k+1)3
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
=[
| k(k+1) |
| 2 |
=(
| k+1 |
| 2 |
=[
| (k+1)(k+2) |
| 2 |
=右边,结论成立
由①②可知,sn=13+23+33+…+n3=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题的考点是数学归纳法,考查类比推理,考查数学归纳法,解题的关键是合理类比,正确运用数学归纳法的证题步骤.

练习册系列答案
相关题目
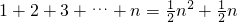 ,若an=n2,则
,若an=n2,则 ,于是,猜想:若an=n3,则sn=13+23+33+…+n3=an4+bn3+cn2+dn.
,于是,猜想:若an=n3,则sn=13+23+33+…+n3=an4+bn3+cn2+dn.