题目内容
(本小题满分10分)
已知函数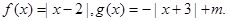
(1)解关于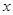 的不等式
的不等式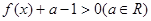 ;
;
(2)若函数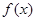 的图象恒在函数
的图象恒在函数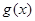 图象的上方,求
图象的上方,求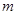 的取值范围。
的取值范围。
已知函数
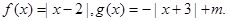
(1)解关于
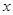 的不等式
的不等式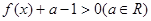 ;
;(2)若函数
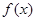 的图象恒在函数
的图象恒在函数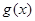 图象的上方,求
图象的上方,求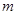 的取值范围。
的取值范围。(1)当 时,不等式的解集是
时,不等式的解集是 ;
;
当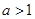 时,不等式的解集为
时,不等式的解集为 ;
;
当 时,即
时,即 ,即
,即 或者
或者 ,即
,即 或者
或者 ,解集为
,解集为 .
.
(2)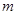 的取值范围是
的取值范围是 .
.
 时,不等式的解集是
时,不等式的解集是 ;
;当
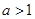 时,不等式的解集为
时,不等式的解集为 ;
;当
 时,即
时,即 ,即
,即 或者
或者 ,即
,即 或者
或者 ,解集为
,解集为 .
.(2)
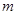 的取值范围是
的取值范围是 .
.试题分析:(1)不等式
 ,即
,即 。
。当
 时,不等式的解集是
时,不等式的解集是 ;
;当
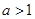 时,不等式的解集为
时,不等式的解集为 ;
;当
 时,即
时,即 ,即
,即 或者
或者 ,即
,即 或者
或者 ,解集为
,解集为 .………(5分)
.………(5分)(2)函数
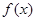 的图象恒在函数
的图象恒在函数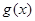 图象的上方,即
图象的上方,即 对任意实数
对任意实数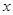 恒成立。即
恒成立。即 对任意实数
对任意实数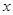 恒成立.
恒成立.由于
 ,故只要
,故只要 .
.所以
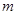 的取值范围是
的取值范围是 .……(10分)
.……(10分)点评:解含绝对值不等式的关键是分区间加以讨论,使含绝对值的不等式转化为不含绝对值的不等式,对于含绝对值的恒成立问题,往往利用分离常数法转化为求解含绝对值不等式的函数最值问题。

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
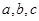 满足
满足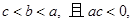 那么
那么



 的解集为( )
的解集为( )



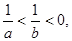 则下列不等式:①
则下列不等式:①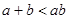 ②
②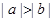 ③
③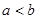 ④
④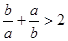 中,正确的不等式有( )
中,正确的不等式有( )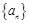 各项均不为0,其前
各项均不为0,其前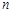 项和为
项和为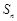 ,且对任意
,且对任意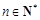 都有
都有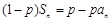 (
(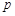 为大于1的常数),记
为大于1的常数),记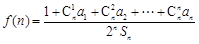 .
.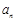 ;
;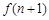 与
与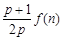 的大小(
的大小(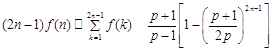
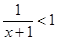 (2)
(2)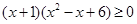
 成立的一个充分不必要条件是
成立的一个充分不必要条件是 ,则实数
,则实数 的取值范围是( )
的取值范围是( )

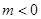 或
或

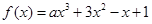 在R上是减函数,求实数
在R上是减函数,求实数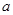 的取值范围。
的取值范围。