题目内容
.(本小题满分12分)设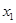 、
、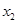
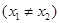 是函数
是函数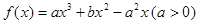 的两个极值点。
的两个极值点。
(1)若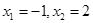 ,求函数
,求函数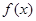 的解析式;
的解析式;
(2)若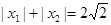 ,求
,求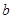 的最大值。
的最大值。
【答案】
(1)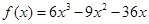 。(2)
。(2)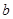 的最大值是
的最大值是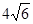 。
。
【解析】本试题主要是考查了导数在研究函数中的运用
(1)利用函数在两个点处取得极值,可知极值点处导数为零得到参数的值。
(2)结合根与系数的关系和参数a,b的值,得到了函数关系式,那么要是等式成立,利用导数得到b的最值。
解:(1)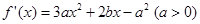
∵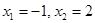 是函数
是函数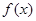 的两个极值点,
的两个极值点,
∴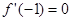 ,
,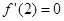 。∴
。∴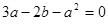 ,
,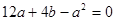 ,解得
,解得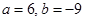 。∴
。∴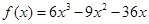 。……4分
。……4分
(2)∵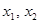 是函数
是函数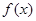 的两个极值点,∴
的两个极值点,∴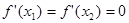 。
。
∴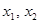 是方程
是方程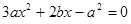 的两根。
的两根。
∵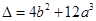 ,∴
,∴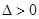 对一切
对一切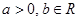 恒成立。
恒成立。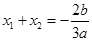 ,
,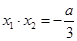 ,……6分
,……6分
∵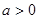 ,∴
,∴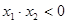 。
。
∴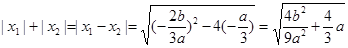
由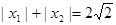 得
得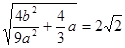 ,∴
,∴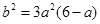 。……8分
。……8分
∵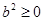 ,∴
,∴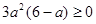 ,∴
,∴ 。令
。令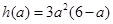 ,则
,则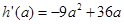 。
。
当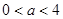 时,
时,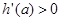 ,∴
,∴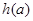 在(0,4)内是增函数;
在(0,4)内是增函数;
当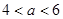 时,
时,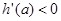 ,∴
,∴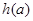 在(4,6)内是减函数。……10分
在(4,6)内是减函数。……10分
∴当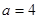 时,
时,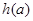 有极大值为96,∴
有极大值为96,∴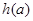 在
在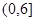 上的最大值是96,
上的最大值是96,
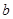 的最大值是
的最大值是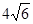 。……12分
。……12分

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目