题目内容
已知一次函数f(x)的图象关于直线y=x对称的图象为C,且f[f(1)]=-1,若点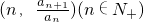 在曲线C上,并有a1=1,
在曲线C上,并有a1=1,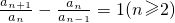
(1)求f(x)的解析式及曲线C的方程;
(2)求数列{an}的通项公式;
(3)设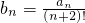 ,求证:数列{bn}的前n项和Sn<
,求证:数列{bn}的前n项和Sn< .
.
解:(1)设f(x)=kx+b(k≠0)(1分)
则f[f(1)]=k(k+b)+b=k2+kb+b=-1即k2+kb+b+1=0①(2分)
又 是曲线C的解析式.
是曲线C的解析式.
∵点 在曲线C上,
在曲线C上,
∴
又∵ 故
故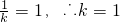 ,代入①得b=-1
,代入①得b=-1
∴f(x)=x-1,f-1(x)=x+1∴曲线C的方程是x-y+1=0(5分)
(2)由(1)知当x=n时,f-1(n)=n+1故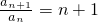 ,而a1=1,
,而a1=1,
于是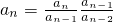
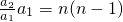 3•2•1=n!(10分)
3•2•1=n!(10分)
(3)∵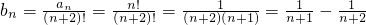
∴Sn=b1+b2++bn=
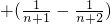 =
= (14分)
(14分)
分析:(1)首先设设f(x)=kx+b(k≠0),代入f[f(1)]即可得k2+kb+b+1=0①;求出反函数 ,将点
,将点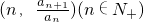 代入得f-1(n)-f-1(n-1)=1,又
代入得f-1(n)-f-1(n-1)=1,又 ,即可得出k=1,代入①得b=-1
,即可得出k=1,代入①得b=-1
故可求出f(x)=x-1,f-1(x)=x+1,进而知曲线C的方程是x-y+1=0;
(2)由(1)知当x=n时,f-1(n)=n+1故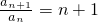 ,即可求出an=n!;
,即可求出an=n!;
(3)由(2)可得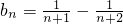 ,即可求出sn=b1+b2++bn=
,即可求出sn=b1+b2++bn= .
.
点评:本题主要考函数及数列的综合运用及其相关运算,属于中档题.
则f[f(1)]=k(k+b)+b=k2+kb+b=-1即k2+kb+b+1=0①(2分)
又
 是曲线C的解析式.
是曲线C的解析式.∵点
 在曲线C上,
在曲线C上,∴

又∵
 故
故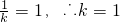 ,代入①得b=-1
,代入①得b=-1∴f(x)=x-1,f-1(x)=x+1∴曲线C的方程是x-y+1=0(5分)
(2)由(1)知当x=n时,f-1(n)=n+1故
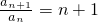 ,而a1=1,
,而a1=1,于是
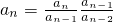
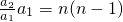 3•2•1=n!(10分)
3•2•1=n!(10分)(3)∵
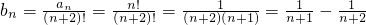
∴Sn=b1+b2++bn=

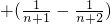 =
= (14分)
(14分)分析:(1)首先设设f(x)=kx+b(k≠0),代入f[f(1)]即可得k2+kb+b+1=0①;求出反函数
 ,将点
,将点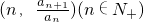 代入得f-1(n)-f-1(n-1)=1,又
代入得f-1(n)-f-1(n-1)=1,又 ,即可得出k=1,代入①得b=-1
,即可得出k=1,代入①得b=-1故可求出f(x)=x-1,f-1(x)=x+1,进而知曲线C的方程是x-y+1=0;
(2)由(1)知当x=n时,f-1(n)=n+1故
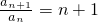 ,即可求出an=n!;
,即可求出an=n!;(3)由(2)可得
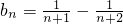 ,即可求出sn=b1+b2++bn=
,即可求出sn=b1+b2++bn= .
.点评:本题主要考函数及数列的综合运用及其相关运算,属于中档题.

练习册系列答案
相关题目