题目内容
在数列 中,
中, ,
, ,则
,则 等于( )
等于( )
 中,
中, ,
, ,则
,则 等于( )
等于( )A. | B. | C. | D. |
B
试题分析:因为
 ,所以
,所以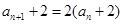 ,
,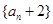 是等比数列
是等比数列首项
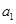 +2=4,公比q=2
+2=4,公比q=2∴
 等于
等于 ,故选B。
,故选B。点评:从一般性的原理出发,推出某个特殊情况下的结论,我们把这种推理称为演绎推理。简言之,演绎推理是由一般到特殊的推理。演绎推理也称为逻辑推理。

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
题目内容
 中,
中, ,
, ,则
,则 等于( )
等于( )A. | B. | C. | D. |
 ,所以
,所以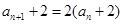 ,
,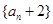 是等比数列
是等比数列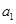 +2=4,公比q=2
+2=4,公比q=2 等于
等于 ,故选B。
,故选B。
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案