题目内容
有一枚正方体骰子,六个面分别写1、2、3、4、5、6的数字,规定“抛掷该枚骰子得到的数字是抛掷后,面向上的那一个数字”.已知 和
和 是先后抛掷该枚骰子得到的数字,函数
是先后抛掷该枚骰子得到的数字,函数

(1)若先抛掷骰子得到的数字是3,求再次抛掷骰子时,使函数 有零点的概率;
有零点的概率;
(2)求函数 在区间(-3,+∞)上是增函数的概率.
在区间(-3,+∞)上是增函数的概率.
【答案】
(1)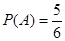 (2)
(2)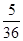
【解析】
试题分析:(1)解:设事件A:再次抛掷骰子时,函数 有零点.
有零点.
若 有零点,则
有零点,则
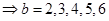 .所以
.所以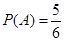 .
.
答:再次抛掷骰子时,函数 有零点的概率为
有零点的概率为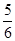 .
.
(2)解:设事件B为函数 在
在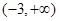 为增函数.
为增函数.
若函数 在
在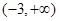 上是增函数,则有
上是增函数,则有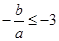 ,即
,即 .
.
当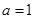 时,
时,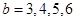 ;当
;当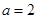 时,
时, .所以
.所以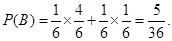
答:函数 在
在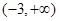 上是增函数的概率是
上是增函数的概率是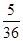 .
.
考点:概率公式;二次函数图象上点的坐标特征.
点评:本题巧妙地把概率、不等式组、二次函数等知识结合在一起,出题思路新颖,别具-格.有利于考查学生灵活应用基础知识解决问题的能力.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 =
= 。
。 有零点的概率;
有零点的概率;