题目内容
（本题满分12分）有一枚正方体骰子，六个面分别写1、2、3、4、5、6的数字，规定“抛掷该枚骰子得到的数字是抛掷后，面向上的那一个数字”。已知b和c是先后抛掷该枚骰子得到的数字，函数
=
。
（Ⅰ）若先抛掷骰子得到的数字是3，求再次抛掷骰子时，使函数
有零点的概率；
（Ⅱ） 求函数在区间（—3，+∞）是增函数的概率
【答案】
：（1）记“函数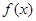
=
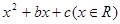有零点”为事件A
由题意知：
，基本事件总数为：（3，1）、（3，2）、
（3，3）、（3， 4）、（3，5）、（3，6）共6个
∵函数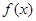=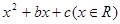有零点， ∴方程
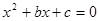有实数根
即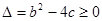
∴
∴ 
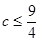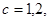
即事件“函数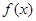=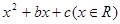有零点”包含2个基本事件
故函数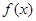=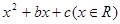有零点的概率P（A）=
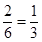………6分
（2）由题意可知：数对
表示的基本事件：（1，1）、（1，2）、（1，3）、（1，4）、（1，5）、（1，6）、（2，1）……（6，5）、（6，6），所以基本事件总数为36。
记“函数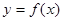
在区间（—3，+∞）是增函数”为事件B。由抛物线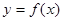的开口向上，使函数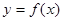在区间（—3，+∞）是增函数，只需
∴ 
∴
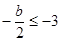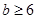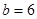
所以事件B包含的基本事件个数为1×6=6个
∴函数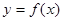在区间（—3，+∞）是增函数的概率P（B）=
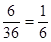………12分
【解析】略
练习册系列答案
相关题目
、2
的分布列及
；
数列
是首项为1，公差为
的等差数列，设
，当
时，求
x，Q=
.今有3万元资金投入经营甲、乙两种商品，为获得最大利润，对甲、乙两种商品的资金投入分别应为多少,能获得的最大利润为多少？
万元和
万元，它们与投入资金万元的关系为：
今有3万元资金投入经营这两种商品，为获得最大利润，对这两种商品的资金分别投入多少时，能获得最大利润？最大利润是多少？