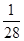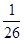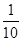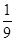题目内容
某工厂统计资料显示,产品次品率p与日产量n (件)(n∈N+,且1≤n≤98)的关系表如下:
| n | 1 | 2 | 3 | 4 | … | 98 |
| p | 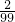 | 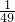 | 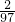 |  | … | 1 |
 元(a>0).
元(a>0).(1)将该厂日盈利额T(元)表示为日产量n(件)的一种函数关系式;
(2)为了获得最大盈利,该厂的日产量应定为多少件?(
 ≈1.73).
≈1.73).
解:(1)由题意可知p=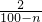 (1≤n≤98,n∈N+).日产量n件中,正品(n-pn)件,
(1≤n≤98,n∈N+).日产量n件中,正品(n-pn)件,
日盈利额T(n)=a(n-pn)- pn=a(n-
pn=a(n-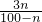 )(1≤n≤98,n∈N+).
)(1≤n≤98,n∈N+).
(2)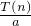 =3+n-
=3+n-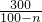 (a>0)=103-[(100-n)+
(a>0)=103-[(100-n)+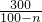 ]≤103-2
]≤103-2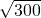 ≈68.4,当且仅当100-n=
≈68.4,当且仅当100-n=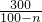 ,
,
即n=100-10 ≈82.7,而n∈N+,且
≈82.7,而n∈N+,且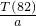 <
<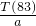 ,
,
故当n=83时,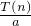 取得最大值,即T取得最大值.
取得最大值,即T取得最大值.
分析:(1)由题意可知p=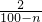 (1≤n≤98,n∈N+).日产量n件中,正品(n-pn)件,从而可得日盈利额函数;
(1≤n≤98,n∈N+).日产量n件中,正品(n-pn)件,从而可得日盈利额函数;
(2)求出日产量函数,利用基本不等式,即可求得结论.
点评:本题考查根据实际问题选择函数类型,根据题意列出函数关系式,并考查利用基本不等式求最值,属于中档题.
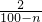 (1≤n≤98,n∈N+).日产量n件中,正品(n-pn)件,
(1≤n≤98,n∈N+).日产量n件中,正品(n-pn)件,日盈利额T(n)=a(n-pn)-
 pn=a(n-
pn=a(n-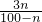 )(1≤n≤98,n∈N+).
)(1≤n≤98,n∈N+).(2)
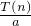 =3+n-
=3+n-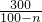 (a>0)=103-[(100-n)+
(a>0)=103-[(100-n)+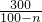 ]≤103-2
]≤103-2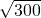 ≈68.4,当且仅当100-n=
≈68.4,当且仅当100-n=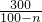 ,
,即n=100-10
 ≈82.7,而n∈N+,且
≈82.7,而n∈N+,且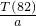 <
<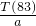 ,
,故当n=83时,
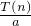 取得最大值,即T取得最大值.
取得最大值,即T取得最大值.分析:(1)由题意可知p=
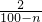 (1≤n≤98,n∈N+).日产量n件中,正品(n-pn)件,从而可得日盈利额函数;
(1≤n≤98,n∈N+).日产量n件中,正品(n-pn)件,从而可得日盈利额函数;(2)求出日产量函数,利用基本不等式,即可求得结论.
点评:本题考查根据实际问题选择函数类型,根据题意列出函数关系式,并考查利用基本不等式求最值,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某工厂统计资料显示,一种产品次品率p与日产量x(x∈N*,80≤x≤100)件之间的关系如下表所示:
其中P(x)=
(a为常数).已知生产一件正品盈利k元,生产一件次品损失
元(k为给定常数).
(1)求出a,并将该厂的日盈利额y(元)表示为日生产量x(件)的函数;
(2)为了获得最大盈利,该厂的日生产量应该定为多少件?
日产量x |
80 |
81 |
82 |
… |
x | … |
98 |
99 |
100 | ||||||||||||
次品率p |
|
|
|
… |
P(x) |
… |
|
|
|
| 1 |
| a-x |
| k |
| 3 |
(1)求出a,并将该厂的日盈利额y(元)表示为日生产量x(件)的函数;
(2)为了获得最大盈利,该厂的日生产量应该定为多少件?
(本小题满分14分)某工厂统计资料显示,一种产品次品率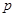 与日产量
与日产量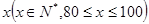 件之间的关系如下表所示:
件之间的关系如下表所示:
|
日产量 |
80 |
81 |
82 |
… |
|
… |
98 |
99 |
100 |
|
次品率 |
|
|
|
… |
P( |
… |
|
|
|
其中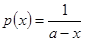 (
(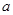 为常数).已知生产一件正品盈利
为常数).已知生产一件正品盈利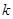 元,生产一件次品损失
元,生产一件次品损失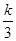 元(
元(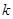 为给定常数).(Ⅰ)求出
为给定常数).(Ⅰ)求出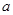 ,并将该厂的日盈利额
,并将该厂的日盈利额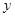 (元)表示为日生产量
(元)表示为日生产量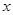 (件)的函数;
(件)的函数;
(Ⅱ)为了获得最大盈利,该厂的日生产量应该定为多少件?