题目内容
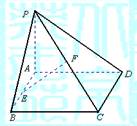
 如图,已知矩形ABCD中,AB=3,BC=a,若PA⊥平面AC,在BC边上取点E,使PE⊥DE,则满足条件的E点有2个时,a的取值范围是( )
如图,已知矩形ABCD中,AB=3,BC=a,若PA⊥平面AC,在BC边上取点E,使PE⊥DE,则满足条件的E点有2个时,a的取值范围是( )分析:由已知中PA⊥平面AC,在BC边上取点E,使PE⊥DE,由线面垂直的判定定理及性质可得满足条件时,AE⊥DE,即E点为以AD为直径的圆与BC的交点,再根据AB=3,BC=a,满足条件的E点有2个,我们可得a的取值范围.
解答:解:∵PA⊥平面AC,
∴PA⊥DE
又∵PE⊥DE,PA∩PE=P
∴DE⊥平面PAE
∴DE⊥AE
即E点为以AD为直径的圆与BC的交点
∵AB=3,BC=a,满足条件的E点有2个
∴a>6
故选A
∴PA⊥DE
又∵PE⊥DE,PA∩PE=P
∴DE⊥平面PAE
∴DE⊥AE
即E点为以AD为直径的圆与BC的交点
∵AB=3,BC=a,满足条件的E点有2个
∴a>6
故选A
点评:本题考查的知识点是空间中直线与直线之间的位置关系,其中根据满足条件时AE⊥DE,即E点为以AD为直径的圆与BC的交点,判断出满足条件的E点有2个,半径大于3,进而得到a的范围,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 BC,FO
BC,FO


 为矩阵
为矩阵 属于λ的一个特征向量,求实数a,λ的值及A2。
属于λ的一个特征向量,求实数a,λ的值及A2。 (α为参数),曲线D的参数方程为
(α为参数),曲线D的参数方程为 ,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
 计20分。请在答题卡指定区域作答。解答应写出文字
计20分。请在答题卡指定区域作答。解答应写出文字 说明、证明过程或演算
说明、证明过程或演算 步骤。
步骤。
 为矩阵
为矩阵 属于λ的一个特征向量,求实数a,λ的值及A2。
属于λ的一个特征向量,求实数a,λ的值及A2。 在平面直角坐标系xoy中,曲线C的参数方程为
在平面直角坐标系xoy中,曲线C的参数方程为 (α为参数),曲线D的参数方程为
(α为参数),曲线D的参数方程为 ,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。 正实数,且ab=2。求证:(1+2a)(1+b)≥9。
正实数,且ab=2。求证:(1+2a)(1+b)≥9。