题目内容
如图,已知在矩形ABCD中,AB=3,BC=4,沿对角线AC将△ABC折起,使B点在平面ADC内的射影恰好落在AD上,求:
(1)异面直线AB与CD成的角;
(2)异面直线AB与CD的距离;
(3)二面角B-AC-D的大小.

答案:
解析:
解析:
|
解 如上图,设B在平面ADC内的射影为F, 则BF⊥平面ADC, 由题意,F在AD上,过F作FE⊥AC于E,连结BE, 则AC⊥BE(三垂线定理). 所以∠BEF为二面角B-AC-D的平面角.设 (1)∵ BF⊥平面ADC,又AD⊥DC, ∴ AB⊥CD(三垂线定理). ∴ 异面直线AB与CD成 (2)过D在平面ABD内作DH⊥AB于H(如上图). ∵ CD⊥平面ABD, ∴ CD⊥DH. 因此DH为异面直线CD、AB的公垂线. 因为 AB·DH=BF·AD, 且AB=3,AD=BC=4, 又由BE·AC=AB·BC,知
∴ AB与CD之间的距离为
|

练习册系列答案
相关题目
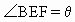 .
.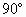 角.
角.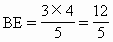 ;
;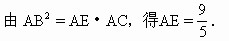
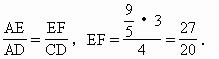
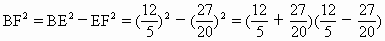
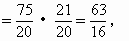
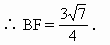
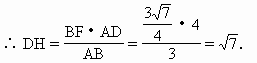
 .
.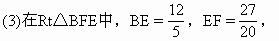
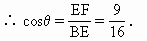
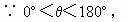
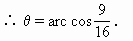
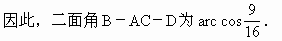
 如图,如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点.
如图,如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点. 如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.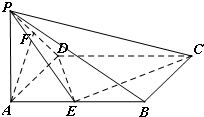 (2012•贵州模拟)如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,F是PD的中点,E是线段AB上的点.
(2012•贵州模拟)如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,F是PD的中点,E是线段AB上的点.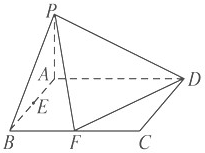 如图,已知在四棱锥PABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.
如图,已知在四棱锥PABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.