题目内容
11.写出与下列各角终边相同的角的集合S,并把S中满足不等式-360°≤α<720°的元素α写出来.(1)100°
(2)-120°
(3)-380°20′.
分析 直接利用角的终边所在象限求解即可.
解答 解:(1)100°,终边所在的集合S={α|α=k360°+100°,k∈Z}.k=-1时,α=-260°;k=0时,α=100°;
k=1时,α=460°;
(2)-120°,终边所在的集合S={α|α=k360°-120°,k∈Z}.k=0时,α=-120°;k=1时,α=240°;
k=2时,α=600°;
(3)-380°20,终边所在的集合S={α|α=k360°-380°12′,k∈Z}.k=1时,α=-20°12′;k=2时,α=339°48′;
k=3时,α=699°48′;
点评 本题考查三角函数角的终边的求法,考查计算能力.

练习册系列答案
相关题目
19.不等式4${\;}^{{x}^{2}}$<23x的解集是( )
| A. | {x|0<x<$\frac{3}{2}$} | B. | {x|0<x<3} | C. | {x|1<x<$\frac{3}{2}$} | D. | {x|$\frac{3}{2}$<x<3| |
16.若α为第二象限角,则2α的终边在( )
| A. | 第一或第二象限 | B. | 第二或第四象限 | ||
| C. | 第三或第四象限 | D. | 第三或第四象限或y轴的非正半轴 |
 的内角
的内角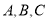 所对的边分别为
所对的边分别为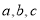 ,向量
,向量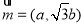 与
与 平行.
平行.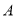 ;
;  求
求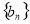 与数列
与数列
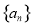 满足
满足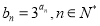
 是何种数列,并给出证明;
是何种数列,并给出证明;