题目内容
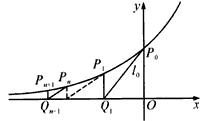
如图,过曲线C:y=ex上一点P0(0,1)作曲线C的切线l2交x轴于点Q1(x1,0),又x轴的垂线交曲线C于点P1(x1,y1),然后再过P1(x1,y1)作曲线C的切线l1交x轴于点Q2(x2,0),又过Q2作x轴的垂线交曲线C于点P2 (x2,y2),……,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1作x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n∈N*),
(1)求x1、x2及数列{xn}的通项公式;
(2)设曲线C与切线ln及直线PQ所围成的图形面积为Sn,求Sn的表达式;
(3)在满足(2)的条件下,若数列{Sn}的前n项和为Tn,求证: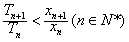 。
。
(1)求x1、x2及数列{xn}的通项公式;
(2)设曲线C与切线ln及直线PQ所围成的图形面积为Sn,求Sn的表达式;
(3)在满足(2)的条件下,若数列{Sn}的前n项和为Tn,求证:
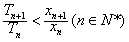 。
。 
(1)解:由y′=ex,设直线ln的斜率为kn,则 ,
,
∴直线ln的方程为y=x+1,
令y=0,得x1=-1,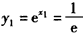 ,
,
∴ ,∴
,∴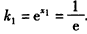 ,
,
∴直线l1的方程为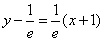 ,
,
令y=0,得x2=-2,
一般地,直线ln的方程为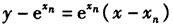 ,
,
由于点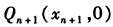 在直线ln上,∴
在直线ln上,∴ ,
,
∴数列{xn}是首项为-1,公差为-1的等差数列,
∴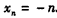 。
。
(2)解: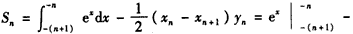
 ;
;
(3)证明: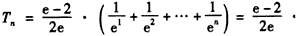
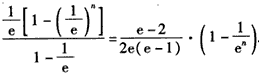 ,
,
∴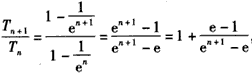 ,
,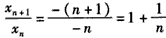 ,
,
要证明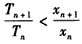 ,
,
只要证明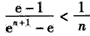 ,
,
即只要证明,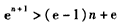 ,
,
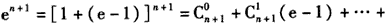
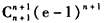
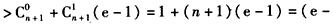
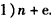 ,
,
∴不等式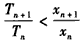 对一切n∈N*都成立.
对一切n∈N*都成立.
 ,
,∴直线ln的方程为y=x+1,
令y=0,得x1=-1,
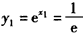 ,
,∴
 ,∴
,∴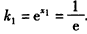 ,
,∴直线l1的方程为
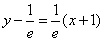 ,
,令y=0,得x2=-2,
一般地,直线ln的方程为
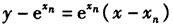 ,
,由于点
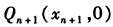 在直线ln上,∴
在直线ln上,∴ ,
,∴数列{xn}是首项为-1,公差为-1的等差数列,
∴
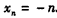 。
。(2)解:
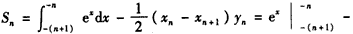
 ;
;(3)证明:
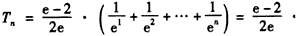
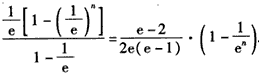 ,
,∴
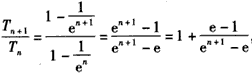 ,
,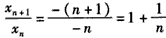 ,
,要证明
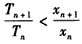 ,
,只要证明
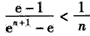 ,
,即只要证明,
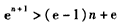 ,
,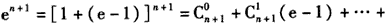
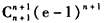
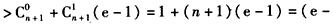
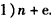 ,
,∴不等式
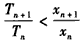 对一切n∈N*都成立.
对一切n∈N*都成立. 
练习册系列答案
相关题目
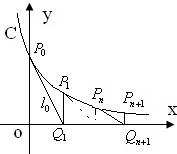 如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).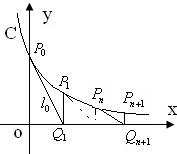 如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).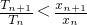 (n∈N+).
(n∈N+).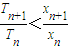 (n∈N+).
(n∈N+).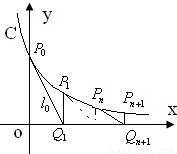
 (n∈N+).
(n∈N+).