题目内容
设集合A={x|
＜0}，若p、q∈A，求方程x2+2px-q2+1=0有两实根的概率．
| x+3 |
| x-3 |
集合A={x|
＜0}={x|-3＜x＜3}，
又∵方程x2+2px-q2+1=0有两个实数根，
∴△≥0，即有：
，
即
．
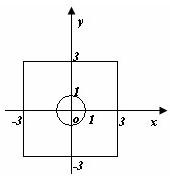
在坐标平面内画出其表示的平面区域，如图所示，是正方形内单位圆外的部分．
其中圆的面积为π，正方形的面积为36，
根据几何概率的计算公式得，
方程x2+2px-q2+1=0有两个实数根的概率：P=
=
．
| x+3 |
| x-3 |
又∵方程x2+2px-q2+1=0有两个实数根，
∴△≥0，即有：
|
即
|
在坐标平面内画出其表示的平面区域，如图所示，是正方形内单位圆外的部分．
其中圆的面积为π，正方形的面积为36，
根据几何概率的计算公式得，
方程x2+2px-q2+1=0有两个实数根的概率：P=
| S圆外的部分 |
| S正方形 |
| 36-π |
| 36 |
练习册系列答案
阅读快车系列答案
相关题目
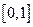上任取两个数
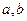，方程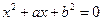
的两根均为实数的概率为 ；
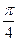
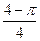
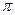
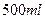的水中有一个草履虫，现从中随机取出
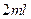水样放到显微镜下观察，则发现草履虫的概率是_____________