题目内容
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值.由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4∶2∶1.
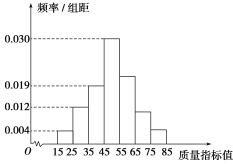
(1)求这些产品质量指标值落在区间[75,85]内的概率;
(2)若将频率视为概率,从该企业生产的这种产品中随机抽取3件,记这3件产品中质量指标值位于区间[45,75)内的产品件数为X,求X的分布列.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)利用已知条件及频率之和为1,即可求出;(2)X的所有可能取值为0,1,2,3,分别求出对应的概率,列出分布列即可.
(1)设这些产品质量指标值落在区间[75,85)内的频率为x,则落在区间[55,65),[65,75)内的频率分别为4x,2x.依题意得(0.004+0.012+0.019+0.030)×10+4x+2x+x=1,解得x=0.05.
所以这些产品质量指标值落在区间[75,85]内的频率为0.05.
(2)从该企业生产的这种产品中随机抽取3件,相当于进行了3次独立重复试验,所以X服从二项分布B(n,p),其中n=3.
由(1)得,这些产品质量指标值落在区间[45,75]内的频率为0.3+0.2+0.1=0.6,将频率视为概率得p=0.6.
因为X的所有可能取值为0,1,2,3,且P(X=0)=![]() ×0.60×0.43=0.064,
×0.60×0.43=0.064,
P(X=1)=![]() ×0.61×0.42=0.288,
×0.61×0.42=0.288,
P(X=2)=![]() ×0.62×0.41=0.432,
×0.62×0.41=0.432,
P(X=3)=![]() ×0.63×0.40=0.216,
×0.63×0.40=0.216,
所以X的分布列为
X | 0 | 1 | 2 | 3 |
P | 0.064 | 0.288 | 0.432 | 0.216 |

【题目】某校为了解高三年级不同性别的学生对取消艺术课的态度(支持或反对),进行了如下的调查研究,全年级共有1350人,男女生比例为![]() ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为![]() ,通过对被抽取学生的问卷调查,得到如下
,通过对被抽取学生的问卷调查,得到如下![]() 列联表:
列联表:
支持 | 反对 | 总计 | |
男生 | 30 | ||
女生 | 25 | ||
总计 |
(1)完成列联表,并判断能否有![]() 的把握认为态度与性别有关?
的把握认为态度与性别有关?
(2)若某班有6名男生被抽到,其中2人支持,4人反对;有4名女生被抽到,其中2人支持,2人反对,现从这10人中随机抽取一男一女进一步调查原因.求其中恰有一人支持一人反对的概率.
参考公式及临界值表:![]()
| 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】现有一款智能学习APP,学习内容包含文章学习和视频学习两类,且这两类学习互不影响,已知该APP积分规则如下:每阅读一篇文章积1分,每日上限积5分;观看视频累计3分钟积2分,每日上限积6分,经过抽样统计发现,文章学习积分的概率分布表如表1所示,视频学习积分的概率分布表如表2所示.
表1
文章学习积分 | 1 | 2 | 3 | 4 | 5 |
概率 |
|
|
|
|
|
表2
视频学习积分 | 2 | 4 | 6 |
概率 |
|
|
|
(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为![]() ,求
,求![]() 的概率分布及数学期望.
的概率分布及数学期望.