题目内容
13.已知实数x,y满足$\left\{\begin{array}{l}{(x-y+6)(x+y-6)≥0}\\{1≤x≤4}\end{array}\right.$(1)求x2+y2-2的取值范围;
(2)求$\frac{y}{x-3}$的取值范围.
分析 (1)利用两点间的距离公式的几何意义进行求解.
(2)利用斜率的公式进行求解.
解答 解:(1)作出不等式组对应的平面区域如图: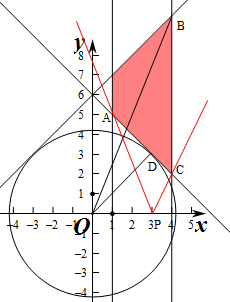
设z=x2+y2-2,d=$\sqrt{{x}^{2}+{y}^{2}}$
则z的几何意义为区域内的点到原点距离的平方减2,即z=d2-2.
由图象知OB的距离最大,点O到直线x+y-6=0的距离OD最小,
由$\left\{\begin{array}{l}{x=4}\\{x-y+6=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=4}\\{y=10}\end{array}\right.$,此时z=42+102-2=114.
点O到直线x+y-6=0的距离OD=$\frac{|-6|}{\sqrt{2}}=3\sqrt{2}$,
此时z=d2-2=(3$\sqrt{2}$)2-2=18-2=16,
故16≤z≤114,
故x2+y2-2的取值范围是[16,114].
(2)设k=$\frac{y}{x-3}$,则k的几何意义是区域内的点到定点P(3,0)的斜率,
由$\left\{\begin{array}{l}{x=1}\\{x+y-6=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=5}\end{array}\right.$,即A(1,5),
由$\left\{\begin{array}{l}{x=4}\\{x+y-6=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,即C(4,2),
则PC的斜率k=$\frac{2}{4-3}=2$,PA的斜率k=$\frac{5}{1-3}$=$-\frac{5}{2}$,
则k≥2或k≤$-\frac{5}{2}$
点评 本题主要考查线性规划的应用,利用数形结合以及两点间的距离公式以及直线的斜率公式是解决本题的关键.

| A. | 9x-16y+7=0 | B. | 16x+9y-25=0 | C. | 9x+16y-25=0 | D. | 16x-9y-7=0 |
| A. | 不存在 | B. | 恰有一条 | C. | 恰有两条 | D. | 有无数条 |
| A. | y=-2x-$\frac{3}{2}$-3ln3 | B. | y=-2x+$\frac{3}{2}$ | C. | y=-2x+$\frac{21}{2}$-3ln3 | D. | y=-2x+$\frac{5}{2}$ |
| A. | 存在唯一直线l,使得l丄 a,且l丄b | B. | 存在唯一直线l,使得l∥a,且l丄b | ||
| C. | 存在唯一平面α,使得 a?α,且 b∥α | D. | 存在唯一平面α,使得a?α,且b丄α |