题目内容
2.已知直线l:y=ax+b与曲线F:x=$\frac{1}{y}$+y没有公共点,若平行于l的直线与曲线F有且只有一个公共点,则符合条件的直线l( )| A. | 不存在 | B. | 恰有一条 | C. | 恰有两条 | D. | 有无数条 |
分析 由直线L和T无公共点,可知平移直线后直线与曲线F相切,即可得到结论.
解答 解:由曲线T:x=$\frac{1}{y}$+y,得$y=\frac{x-\sqrt{{x}^{2}-4}}{2}$或$y=\frac{x+\sqrt{{x}^{2}-4}}{2}$.
∵直线L:y=ax+b与曲线T:x=$\frac{1}{y}$+y没有公共点,
∴直线y=ax+b与双曲线的渐近线平行,
∴平移后直线y=ax+b与曲线F相切,
各有一条切线,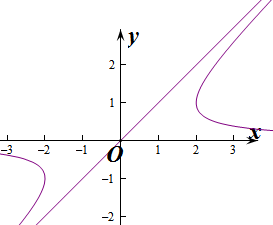
∴平行L的直线与曲线T有且只有一个公共点的直线有2条,
故选:C
点评 本题主要考查直线和圆锥曲线的位置关系的判断,利用条件转化切线问题是解决本题的关键.

练习册系列答案
相关题目
 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,M为棱AC中点.AB=BC,AC=2,AA1=$\sqrt{2}$.