题目内容
已知定义在实数集上的函数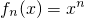 ,n∈N*,其导函数记为f′n(x),且满足.
,n∈N*,其导函数记为f′n(x),且满足.
(Ⅰ)设函数g(x)=f2n-1(x)•fn(1-x),求g(x)的极大值与极小值;
(Ⅱ)试求关于x的方程 在区间(0,1)上的实数根的个数.
在区间(0,1)上的实数根的个数.
解:(Ⅰ)∵y=g(x)=f2n-1(x)•fn(1-x)=(1-x)n•x2n-1,
则y′=-n(1-x)n-1•x2n-1+(2n-1)x2n-2•(1-x)n=x2n-2•(1-x)n-1[(2n-1)-(3n-1)x],…(3分)
令y′=0,得x1=0,x2= ,x3=1,且x1<x2<x3,
,x3=1,且x1<x2<x3,
当n为正偶数时,随x的变化,y′与y的变化如下:
所以当x= 时,y极大=
时,y极大= ;当x=1时,y极小=0.
;当x=1时,y极小=0.
当n为正奇数时,随x的变化,y'与y的变化如下:
所以x= 时,y极大=
时,y极大= ;无极小值.
;无极小值.
(II) =
=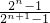 ,即
,即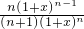 =
=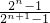 (x≠-1),
(x≠-1),
所以方程为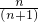 •
• =
=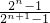 (x≠-1),
(x≠-1),
∴x=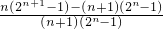 =
=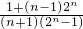 >0,
>0,
又x-1=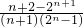 ,而对于n∈N*,有2n+1>n+2(利用二项式定理可证),
,而对于n∈N*,有2n+1>n+2(利用二项式定理可证),
∴x<1.
综上,对于任意给定的正整数n,方程只有唯一实根,且总在区间(0,1)内,所以原方程在区间(0,1)上有唯一实根.
分析:(Ⅰ)依题意,可求得g′(x),令g′(x)=0,得x1=0,x2= ,x3=1,且x1<x2<x3,分n为正偶数与n为正奇数讨论,随x的变化,y′与y的变化情况即可求g(x)的极大值与极小值;
,x3=1,且x1<x2<x3,分n为正偶数与n为正奇数讨论,随x的变化,y′与y的变化情况即可求g(x)的极大值与极小值;
(Ⅱ)依题意,可求得x=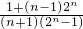 >0,对于n∈N*,有2n+1>n+2,于是x-1=
>0,对于n∈N*,有2n+1>n+2,于是x-1=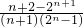 <0,从而可求得0<x<1,于是在区间(0,1)上方程只有唯一实根.
<0,从而可求得0<x<1,于是在区间(0,1)上方程只有唯一实根.
点评:本题考查利用导数研究函数的极值,考查根的存在性及根的个数判断,(Ⅰ)中对n分n为正偶数与n为正奇数讨论,随x的变化,y′与y的变化情况求g(x)的值是难点,考查推理分析与复杂的运算能力,属于难题.
则y′=-n(1-x)n-1•x2n-1+(2n-1)x2n-2•(1-x)n=x2n-2•(1-x)n-1[(2n-1)-(3n-1)x],…(3分)
令y′=0,得x1=0,x2=
 ,x3=1,且x1<x2<x3,
,x3=1,且x1<x2<x3,当n为正偶数时,随x的变化,y′与y的变化如下:
| x | (-∞,0) | 0 | (0, ) ) |  | ( ,1) ,1) | (1,+∞) | |
| y′ | + | 0 | + | 0 | - | 0 | + |
| y | 极大值 | 极小值 |
 时,y极大=
时,y极大= ;当x=1时,y极小=0.
;当x=1时,y极小=0.当n为正奇数时,随x的变化,y'与y的变化如下:
| x | (-∞,0) | 0 | (0, ) ) |  | ( ,1) ,1) | (1,+∞) | |
| y′ | + | 0 | + | 0 | - | 0 | + |
| y | 极大值 |
 时,y极大=
时,y极大= ;无极小值.
;无极小值.(II)
 =
=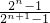 ,即
,即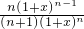 =
=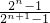 (x≠-1),
(x≠-1),所以方程为
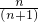 •
• =
=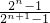 (x≠-1),
(x≠-1),∴x=
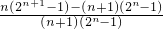 =
=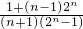 >0,
>0,又x-1=
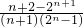 ,而对于n∈N*,有2n+1>n+2(利用二项式定理可证),
,而对于n∈N*,有2n+1>n+2(利用二项式定理可证),∴x<1.
综上,对于任意给定的正整数n,方程只有唯一实根,且总在区间(0,1)内,所以原方程在区间(0,1)上有唯一实根.
分析:(Ⅰ)依题意,可求得g′(x),令g′(x)=0,得x1=0,x2=
 ,x3=1,且x1<x2<x3,分n为正偶数与n为正奇数讨论,随x的变化,y′与y的变化情况即可求g(x)的极大值与极小值;
,x3=1,且x1<x2<x3,分n为正偶数与n为正奇数讨论,随x的变化,y′与y的变化情况即可求g(x)的极大值与极小值;(Ⅱ)依题意,可求得x=
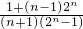 >0,对于n∈N*,有2n+1>n+2,于是x-1=
>0,对于n∈N*,有2n+1>n+2,于是x-1=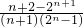 <0,从而可求得0<x<1,于是在区间(0,1)上方程只有唯一实根.
<0,从而可求得0<x<1,于是在区间(0,1)上方程只有唯一实根.点评:本题考查利用导数研究函数的极值,考查根的存在性及根的个数判断,(Ⅰ)中对n分n为正偶数与n为正奇数讨论,随x的变化,y′与y的变化情况求g(x)的值是难点,考查推理分析与复杂的运算能力,属于难题.

练习册系列答案
相关题目