题目内容
5、在正四棱锥P-ABCD中,若侧面与底面所成二面角的大小为60°,则异面直线PA与BC所成角的大小等于
arctan2
.(结果用反三角函数值表示)分析:先通过平移将两条异面直线平移到同一个起点A,得到的锐角或直角就是异面直线所成的角,在三角形中再利用余弦定理求出此角即可.
解答: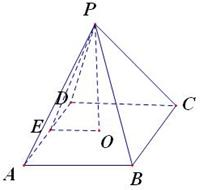 解:如图,取AD的中点E,作PO⊥面ABCD
解:如图,取AD的中点E,作PO⊥面ABCD
则∠PEO=60°,设AB=2,则EO=1,PE=2,AE=1
将BC平移到AD,∠PAD为异面直线PA与BC所成角
tan∠PAD=2,∴∠PAD=arctan2,
故答案为arctan2
 解:如图,取AD的中点E,作PO⊥面ABCD
解:如图,取AD的中点E,作PO⊥面ABCD则∠PEO=60°,设AB=2,则EO=1,PE=2,AE=1
将BC平移到AD,∠PAD为异面直线PA与BC所成角
tan∠PAD=2,∴∠PAD=arctan2,
故答案为arctan2
点评:本小题主要考查异面直线所成的角、直线与平面垂直、二面角等基础知识,考查空间想象能力,运算能力和推理论证能力.

练习册系列答案
相关题目

