题目内容
本题满分12分)在一个盒子中装有6支圆珠笔,其中3支一等品,2支二等品和1支三等品,从中任取3支﹒求
(Ⅰ)恰有1支一等品的概率;
(Ⅱ)没有三等品的概率﹒
(Ⅰ)恰有1支一等品的概率;
(Ⅱ)没有三等品的概率﹒
P(A)=P(A1)+P(A2)=
P(B)=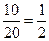

P(B)=
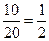
解:(Ⅰ)从6枝圆珠笔中任取3枝为一个基本事件
则全部基本事件的总数为20
恰有1枝一等品的情况记为事件A,
用A1表示1枝一等品,1枝二等品和1枝三等品
用A2表示1枝一等品,2枝二等品,
则A1,A2是互不相容事件,且A=A1+A2,
因为A1中的基本事件的个数为3×2×1=6,A2中的基本事件的个数为3×1=3,∴P(A)=P(A1)+P(A2)= ﹒
﹒
(Ⅱ)没有三等品的情况记为事件B,
因为B中的基本事件的个数为从5枝一等品和二等品中任取3枝,共10种,∴P(B)=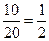
则全部基本事件的总数为20
恰有1枝一等品的情况记为事件A,
用A1表示1枝一等品,1枝二等品和1枝三等品
用A2表示1枝一等品,2枝二等品,
则A1,A2是互不相容事件,且A=A1+A2,
因为A1中的基本事件的个数为3×2×1=6,A2中的基本事件的个数为3×1=3,∴P(A)=P(A1)+P(A2)=
 ﹒
﹒ (Ⅱ)没有三等品的情况记为事件B,
因为B中的基本事件的个数为从5枝一等品和二等品中任取3枝,共10种,∴P(B)=
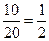

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
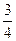 与
与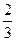 , 设甲投4球恰好投进3球的概率为
, 设甲投4球恰好投进3球的概率为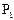 ,乙投3球恰好投进2球的概率为
,乙投3球恰好投进2球的概率为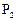 .则
.则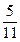
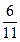
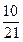
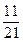
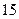 个球,其中
个球,其中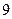 个红球,
个红球,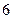 个白球,甲、乙两人各摸一球,不放回,则在甲摸出红球的条件下,乙摸出白球的概率为( )
个白球,甲、乙两人各摸一球,不放回,则在甲摸出红球的条件下,乙摸出白球的概率为( )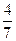
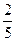

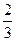
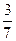
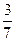 B
B 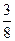 C
C 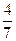 D
D 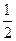


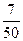

 在复平面上对应的点为
在复平面上对应的点为 .设集合
.设集合 ,
, ,从集合
,从集合 中随机取一个数作为
中随机取一个数作为 ,从集合
,从集合 中随机取一个数作为
中随机取一个数作为 ,求点
,求点