题目内容
抛物线y＝－
x2上有两点A(x1，－x
)，B(x2，－x
)，且
⊥
(O为坐标原点)，
＝(0，－2)
.
(1)求证：
∥
；
(2)若
＝－2
，求△ABO的面积.
(1)＝－＝(－x1，－2＋x)，
＝－＝(x2－x1，－x＋x).
∵⊥，∴·＝x1·x2＋
xx＝0，
∴x1x2(4＋x1x2)＝0，
∴x1x2＝0(舍)或x1x2＝－4，
∴－x1[－(x－x)]＝x1(x2－x1)(x2＋x1)
＝(x2－x1)(x1x2＋x)
＝(－2＋x)(x2－x1).
∴(x2－x1)(－2＋x)＋x1[－(x－x)]＝0，
∴∥.
(2)＝(x1，－x＋2)，＝(x2，－x＋2)
∵＝－2，
∴
⇒
⇒
，
∵⊥，
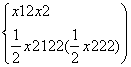∴S△ABO＝||||
＝
·
＝
＝3
.
练习册系列答案
相关题目
x2＋a上，若直线AB的方程为y＝2x＋b(b＞0)，求当b取何值时，△ABP的面积有最大值，并求出最大值．
与x轴正半轴相交于点A，设f(n)为该抛物线在点A处的切线在y轴上的截距．
≥
成立的a的最小值；
与
·
的大小，并说明理由．
与x轴正半轴相交于点A，设f(n)为该抛物线在点A处的切线在y轴上的截距．
≥
成立的a的最小值；
与6·
的大小，并说明理由．