题目内容

解答题

点A、B和P(2，4)都在抛物线y＝－x2＋a上，若直线AB的方程为y＝2x＋b(b＞0)，求当b取何值时，△ABP的面积有最大值，并求出最大值．

答案：
解析：

　　把点(2，4)代入抛物线方程得a＝6，把直线方程y＝2x＋b代入y2＝－x2＋6，得x2＋4x＋2b－12＝0．

　　∴x1＋x2＝－4，x1x2＝2b－12，

　　∴|AB|＝·．

　　又点P(2，4)到直线y＝2x＋b距离为d＝．

　　∴S△ABP＝·|AB|·d＝b＝≤＝；

　　当且仅当b＝16－2b，即b＝时取“＝”．

　　∴当b＝时，S△ABP有最大值．


练习册系列答案
相关题目
选作题，本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
A．（几何证明选讲）
如图，已知两圆交于A、B两点，过点A、B的直线分别与两圆交于P、Q和M、N．求证：PM∥QN．
B．（矩阵与变换）
已知矩阵A的逆矩阵A-1=
10
02
，求矩阵A．
C．（极坐标与参数方程）
在平面直角坐标系xOy中，过椭圆
x2
12
+
y2
4
=1在第一象限处的一点P（x，y）分别作x轴、y轴的两条垂线，垂足分别为M、N，求矩形PMON周长最大值时点P的坐标．
D．（不等式选讲）
已知关于x的不等式|x-a|+1-x＞0的解集为R，求实数a的取值范围．

设点A和B为抛物线＝4px(p＞0)上原点以外的两个动点，已知：OA⊥OB，OM⊥AB，求点M的轨迹方程，并说明它是什么曲线．

解答题：解答应写出文字说明，证明过程或演算步骤．

已知f(x)＝x3－ax2＋b(a，b∈R且a≠0，x∈R)．

(1)

试问函数y＝f(x)在a＞0的条件下，在[1，＋∞)上能否单调递减？

(2)

若函数y＝f(x)的图像在点P(1，0)处的切线与直线3x＋y＝0平行，求常数a，b的值．

(3)

在(2)的条件下，求函数f(x)在区间[0，t](t＞0)上最小值和最大值．
选作题，本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
A．（几何证明选讲）
如图，已知两圆交于A、B两点，过点A、B的直线分别与两圆交于P、Q和M、N．求证：PM∥QN．
B．（矩阵与变换）
已知矩阵A的逆矩阵A-1=，求矩阵A．
C．（极坐标与参数方程）
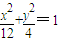在平面直角坐标系xOy中，过椭圆在第一象限处的一点P（x，y）分别作x轴、y轴的两条垂线，垂足分别为M、N，求矩形PMON周长最大值时点P的坐标．
D．（不等式选讲）
已知关于x的不等式|x-a|+1-x＞0的解集为R，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网