题目内容
已知函数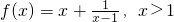 ,且不等式f(x)≥a2+b2+c2对任意x>1恒成立.
,且不等式f(x)≥a2+b2+c2对任意x>1恒成立.
(Ⅰ)试求函数f(x)的最小值;
(Ⅱ)试求a+2b+2c的最大值.
解:(Ⅰ)∵x>1,x-1>0
∴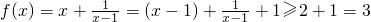
(当且仅当x=2时取“=”号)
∴函数f(x)的最小值3
(Ⅱ)由(Ⅰ)得 a2+b2+c2≤3
由柯西不等式得(a2+b2+c2)(12+22+22)≥(1•a+2•b+2•c)2
∴(a+2b+2c)2≤3×9=27,
∴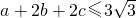 .
.
当且仅当 即
即 时取“=”.
时取“=”.
∴a+2b+2c的最大值 .
.
分析:(Ⅰ)由于x>1,x-1>0根据基本不等式即可求出函数f(x)的最小值.
(Ⅱ)由(Ⅰ)得 a2+b2+c2≤3由柯西不等式得a+2b+2c的最大值.
点评:本小题主要考查柯西不等式在函数极值中的应用、基本不等式等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
∴
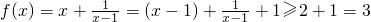
(当且仅当x=2时取“=”号)
∴函数f(x)的最小值3
(Ⅱ)由(Ⅰ)得 a2+b2+c2≤3
由柯西不等式得(a2+b2+c2)(12+22+22)≥(1•a+2•b+2•c)2
∴(a+2b+2c)2≤3×9=27,
∴
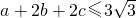 .
.当且仅当
 即
即 时取“=”.
时取“=”.∴a+2b+2c的最大值
 .
.分析:(Ⅰ)由于x>1,x-1>0根据基本不等式即可求出函数f(x)的最小值.
(Ⅱ)由(Ⅰ)得 a2+b2+c2≤3由柯西不等式得a+2b+2c的最大值.
点评:本小题主要考查柯西不等式在函数极值中的应用、基本不等式等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
相关题目
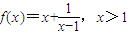 ,且不等式f(x)≥a2+b2+c2对任意x>1恒成立.
,且不等式f(x)≥a2+b2+c2对任意x>1恒成立.