Question

【题目】若动点到定点与定直线的距离之和为4.

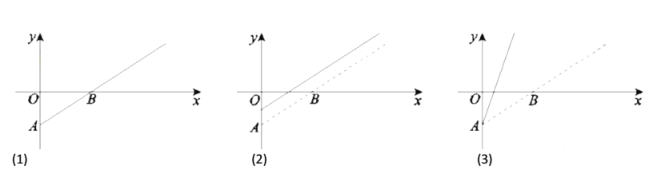
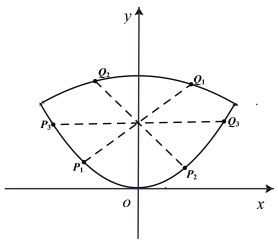
(1)求点的轨迹方程，并画出方程的曲线草图.

(2)记(1)得到的轨迹为曲线，若曲线上恰有三对不同的点关于点对称，求的取值范围.

Answer 1

【答案】(1)，见解析 ；(2).

【解析】

(1)设,由题意,分类讨论后可得点的轨迹方程，并可画出方程的曲线草图.

(2)考虑方程组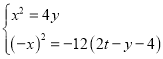在 有两组不同解后可得的取值范围.

(1)设,由题意，

①当时，有，化简得：.

②当时，有，化简得：.

综上所述：点M的轨迹方程为，曲线如图所示.

(2)若,则，

所以曲线关于轴对称，所以一定存在关于轴对称的对称点，

设是轨迹上一点，则,

它关于的对称点为，由于点Q在轨迹上，

所以，

联立方程组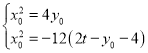(*)得，

化简得,，

当时,，此时方程组(*)有两解,即增加有两组对称点，

所以t的取值范围是.