题目内容
已知函数 在区间[0,1]上单调递增,在区间[1,2]上单调递减。
在区间[0,1]上单调递增,在区间[1,2]上单调递减。
(1)求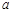 的值;
的值;
(2)若斜率为24的直线是曲线 的切线,求此直线方程;
的切线,求此直线方程;
(3)是否存在实数b,使得函数 的图象与函数
的图象与函数 的图象恰有2个不同交点?若存在,求出实数b的值;若不存在,试说明理由.
的图象恰有2个不同交点?若存在,求出实数b的值;若不存在,试说明理由.
【答案】
(1)由已知得, ,
, ,
, 。
。
(2) ,即
,即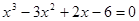 ,
, ,
,
 ,此切线方程为:
,此切线方程为: ,即
,即 。
。
(3)令 ,则
,则
由 得:
得: --------(*)
--------(*)
 ,
,
当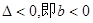 时,(*)无实根,f(x)与g(x)的图象只有1个交点;
时,(*)无实根,f(x)与g(x)的图象只有1个交点;
当 时,(*)的实数解为x=2,
f(x)与g (x)的图象有2个交点;
时,(*)的实数解为x=2,
f(x)与g (x)的图象有2个交点;
当 时,若x=0是(*)的根,则b=4,方程的另一根为x=4,此时,f(x)与g(x)的图象有2个交点;当
时,若x=0是(*)的根,则b=4,方程的另一根为x=4,此时,f(x)与g(x)的图象有2个交点;当 时,f(x)与g(x)的图象有3个不同交点。
时,f(x)与g(x)的图象有3个不同交点。
综上,存在实数b=0或4,使函数f(x)与g(x)的图象恰有2个不同交点。
【解析】略

练习册系列答案
相关题目
 (3)是否存在实数b,使函数
(3)是否存在实数b,使函数 在区间(0,1)内连续,且
在区间(0,1)内连续,且 .
.

 在区间[0,1]上有最小值-2,求
在区间[0,1]上有最小值-2,求 的值.
的值. 在区间[0,1]上的最大值是2,求实数a的值.
在区间[0,1]上的最大值是2,求实数a的值. 在区间(0,1)内连续,且
在区间(0,1)内连续,且 .
.
