题目内容
设a,b,c均为非零向量,且满足条件a+b=c,a-b=d;若向量c⊥d,则一定有( )A.a=b B.|a|=|b| C.a⊥b D.|a|=|b|且a⊥b
解析:因为(a+b)⊥(a-b),所以以a,b为邻边的平行四边形为菱形,因此|a|=|b|,故选B.
答案:B

练习册系列答案
相关题目
设f(x)=asin(πx+α)+bcos(πx+β)+4,其中a、b、α、β均为非零实数,若f(1988)=3,则f(2013)的值为( )
|
| A. | 1 | B. | 5 | C. | 3 | D. | 不确定 |
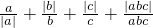 的所有值为元素组成集合是________.
的所有值为元素组成集合是________.