题目内容
设a，b，c均为非零实数，则x=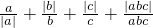
的所有值为元素组成集合是________．
{0，4，-4}
分析：分别讨论a，b，c的不同取值，确定x的取值，然后利用列举法表示集合．
解答：若a，b，c都为正数，则x=1+1+1+1=4．
若a，b，c都为负数，则x=-（1+1+1+1）=-4．
若a，b，c中两正一负，不妨设a＞0，b＞0，c＜0，则abc＜0，所以x=1+1-1-1=0．
若a，b，c中一正两负，不妨设a＞0，b＜0，c＜0，则abc＞0，所以x=1-1-1+1=0．
综上x=0，4，-4．
所以所求的集合为{0，4，-4}．
故答案为：{0，4，-4}．
点评：本题考查了利用列举法表示集合，考查了分类讨论的数学思想，解答的关键是正确讨论a，b，c的各种取值情况．
分析：分别讨论a，b，c的不同取值，确定x的取值，然后利用列举法表示集合．
解答：若a，b，c都为正数，则x=1+1+1+1=4．
若a，b，c都为负数，则x=-（1+1+1+1）=-4．
若a，b，c中两正一负，不妨设a＞0，b＞0，c＜0，则abc＜0，所以x=1+1-1-1=0．
若a，b，c中一正两负，不妨设a＞0，b＜0，c＜0，则abc＞0，所以x=1-1-1+1=0．
综上x=0，4，-4．
所以所求的集合为{0，4，-4}．
故答案为：{0，4，-4}．
点评：本题考查了利用列举法表示集合，考查了分类讨论的数学思想，解答的关键是正确讨论a，b，c的各种取值情况．
练习册系列答案
相关题目
设f（x）=asin（πx+α）+bcos（πx+β）+4，其中a、b、α、β均为非零实数，若f（1988）=3，则f（2013）的值为（ ）
|
| A． | 1 | B． | 5 | C． | 3 | D． | 不确定 |